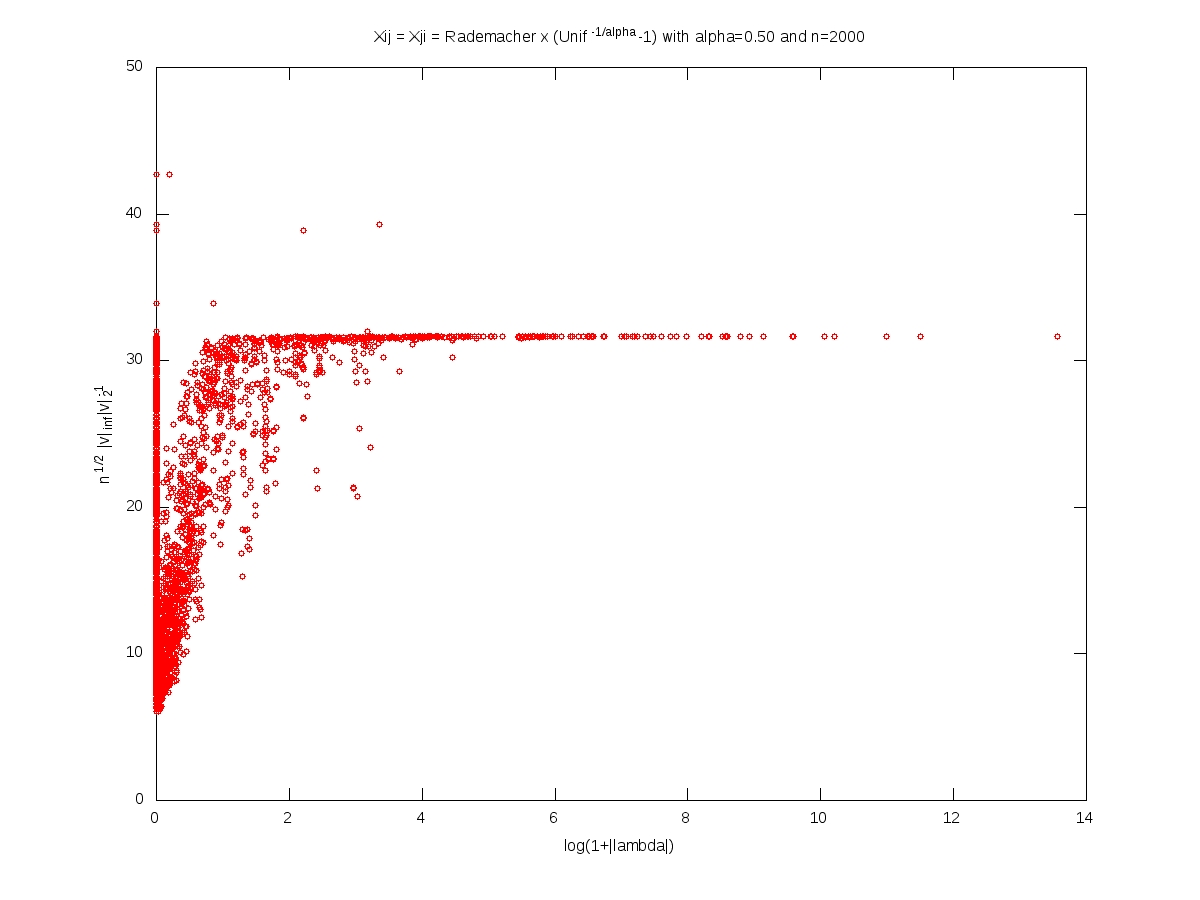
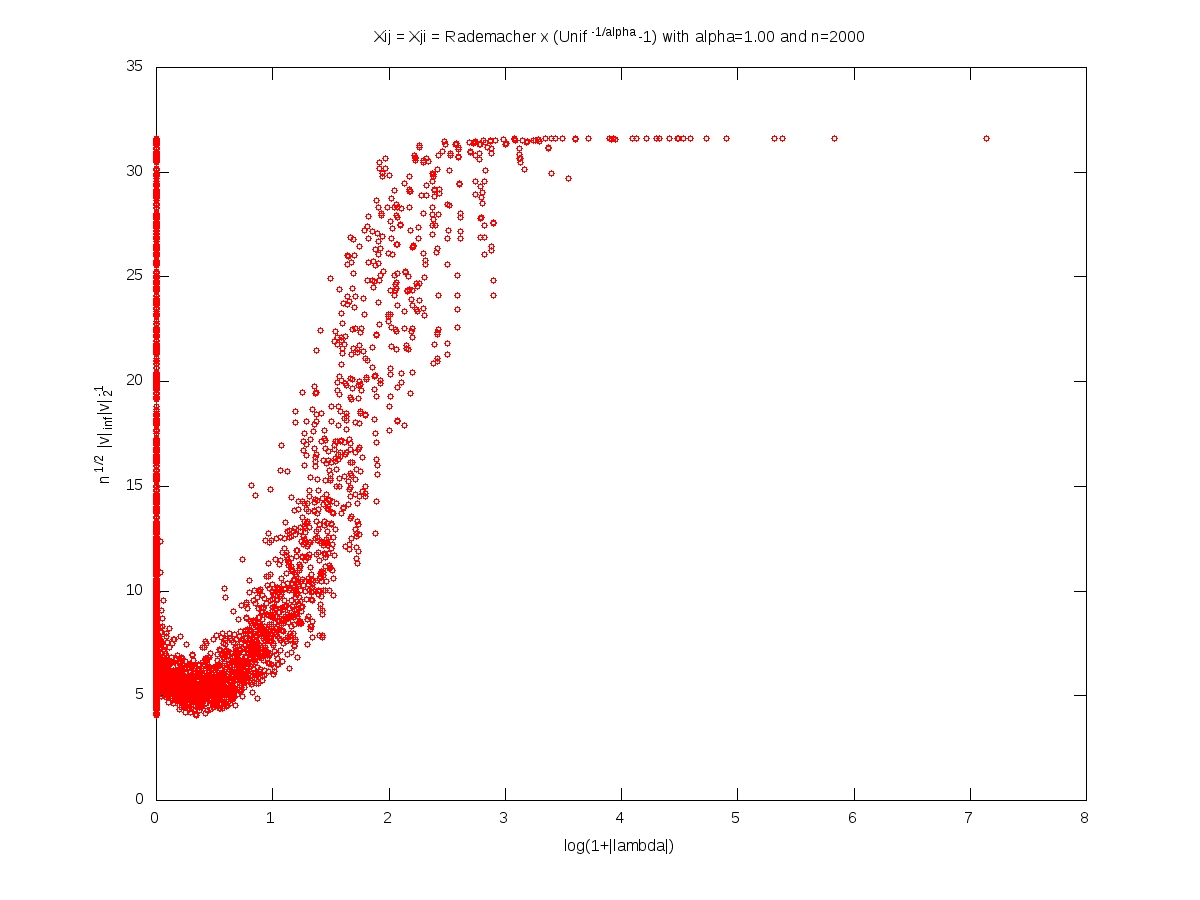
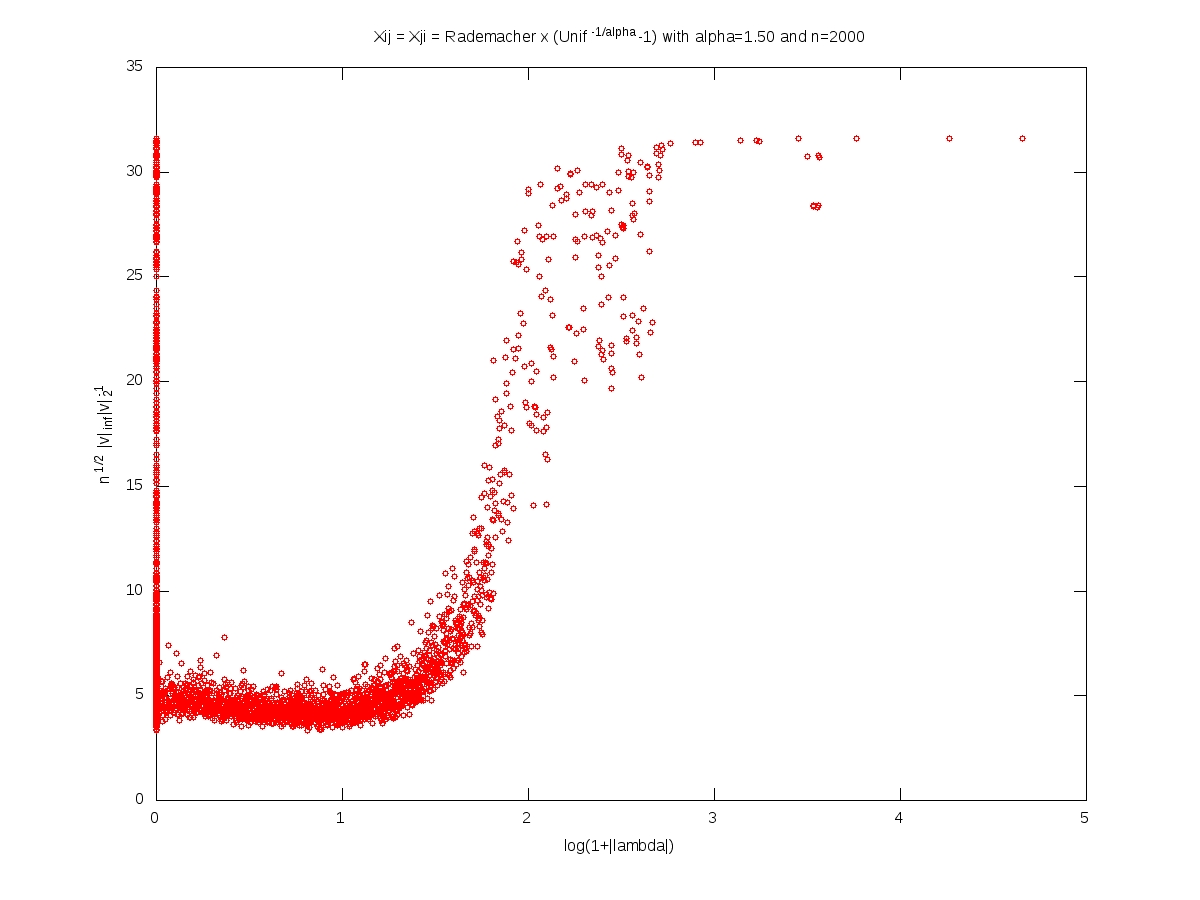
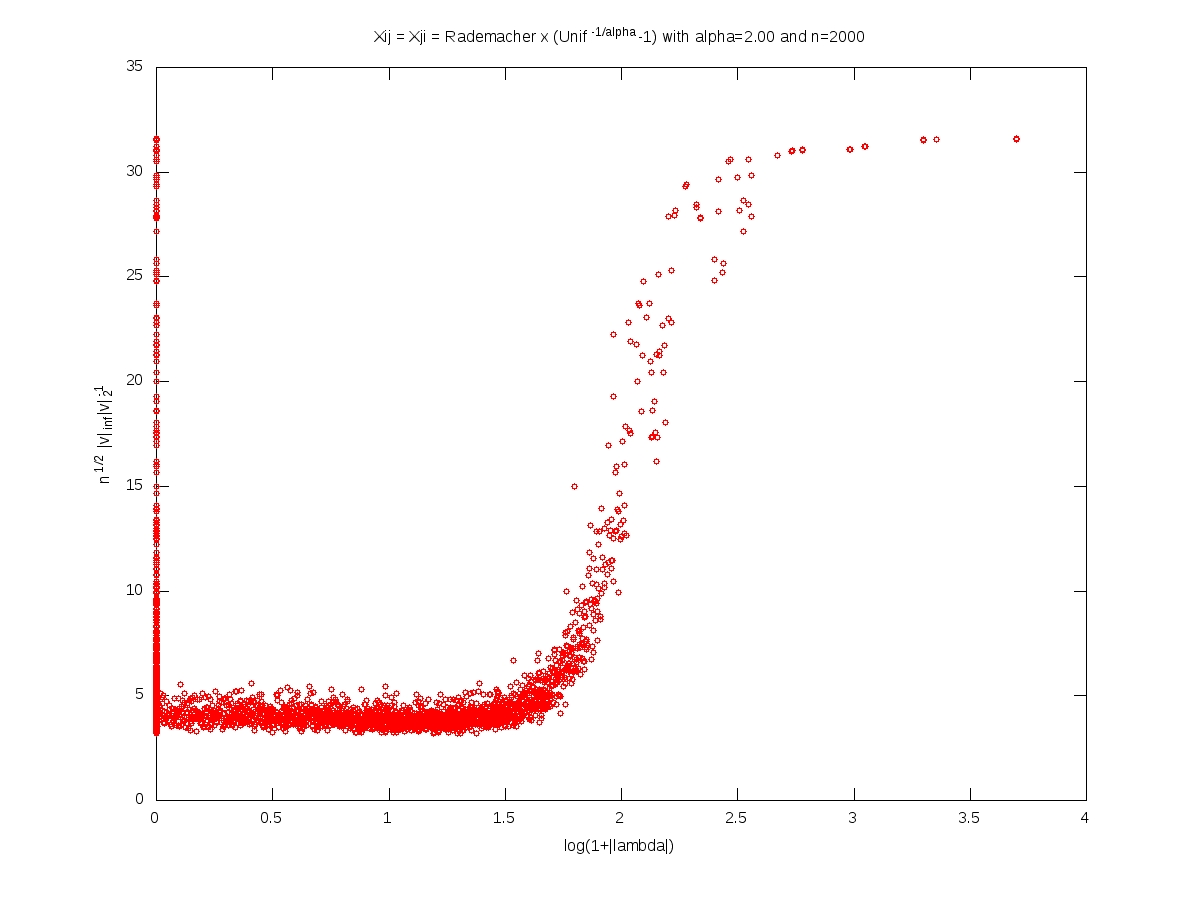
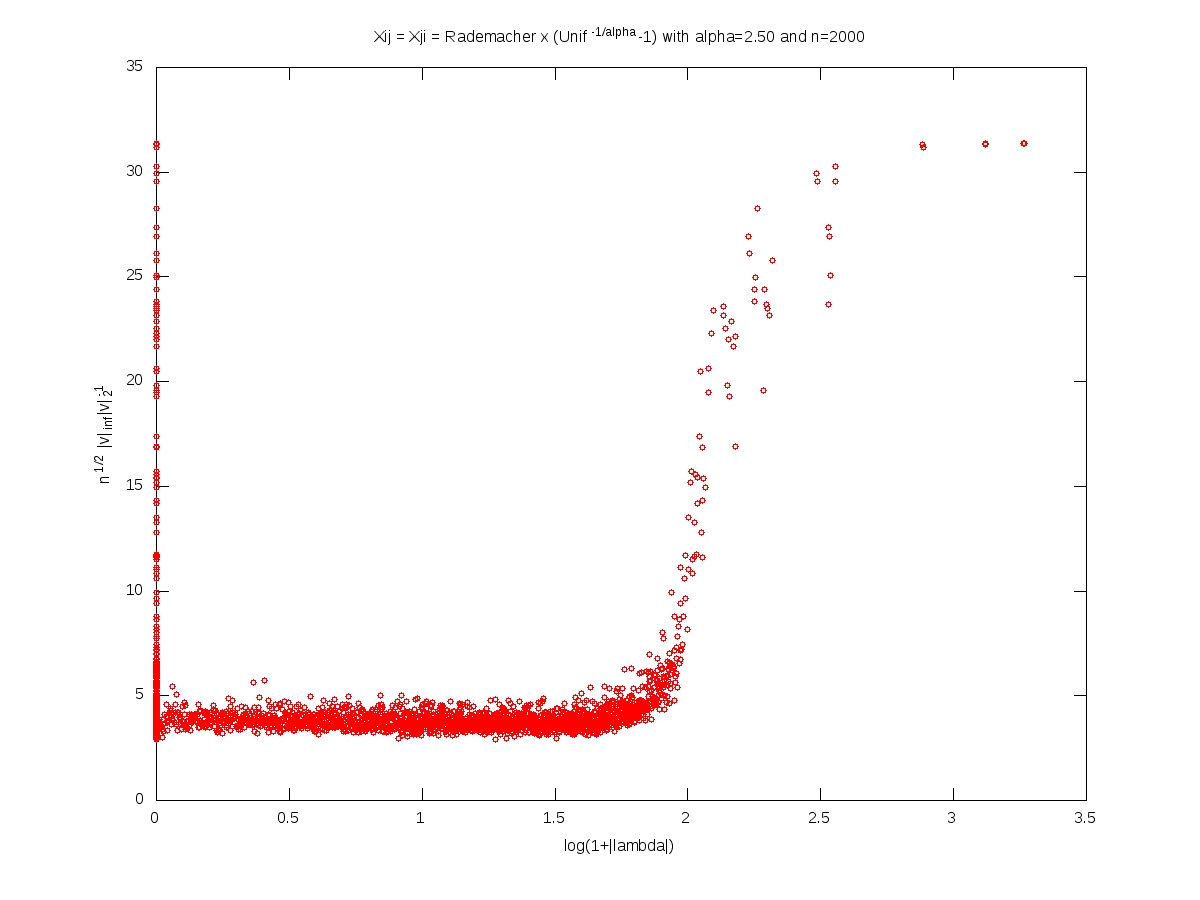
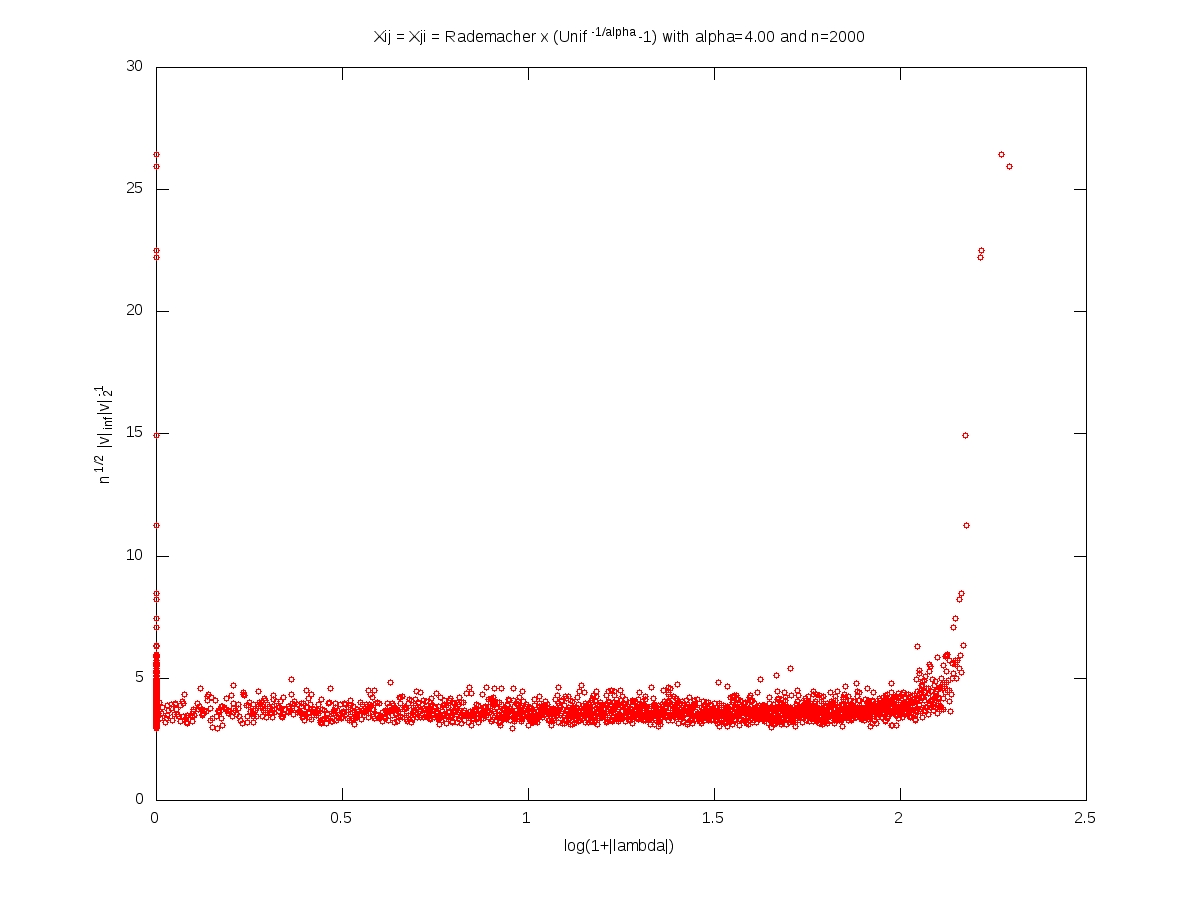
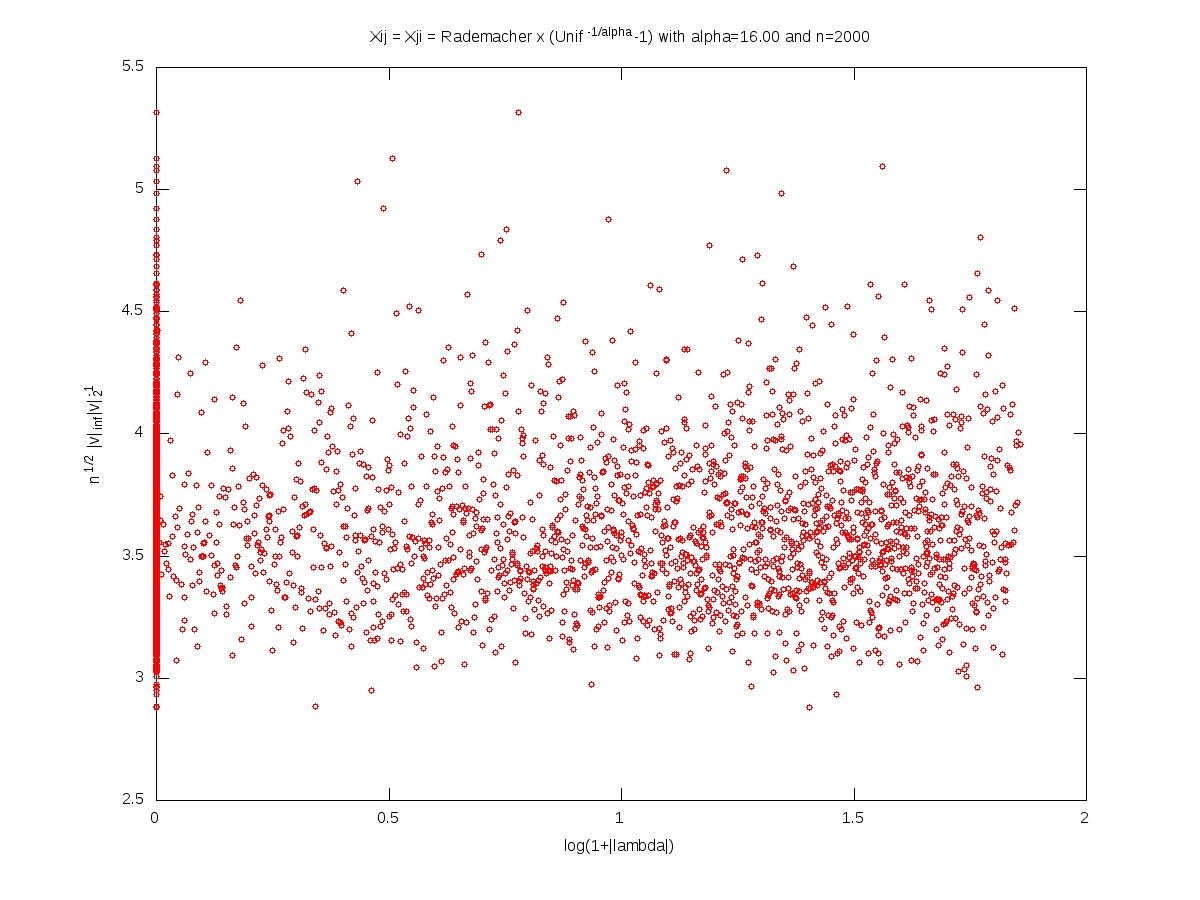
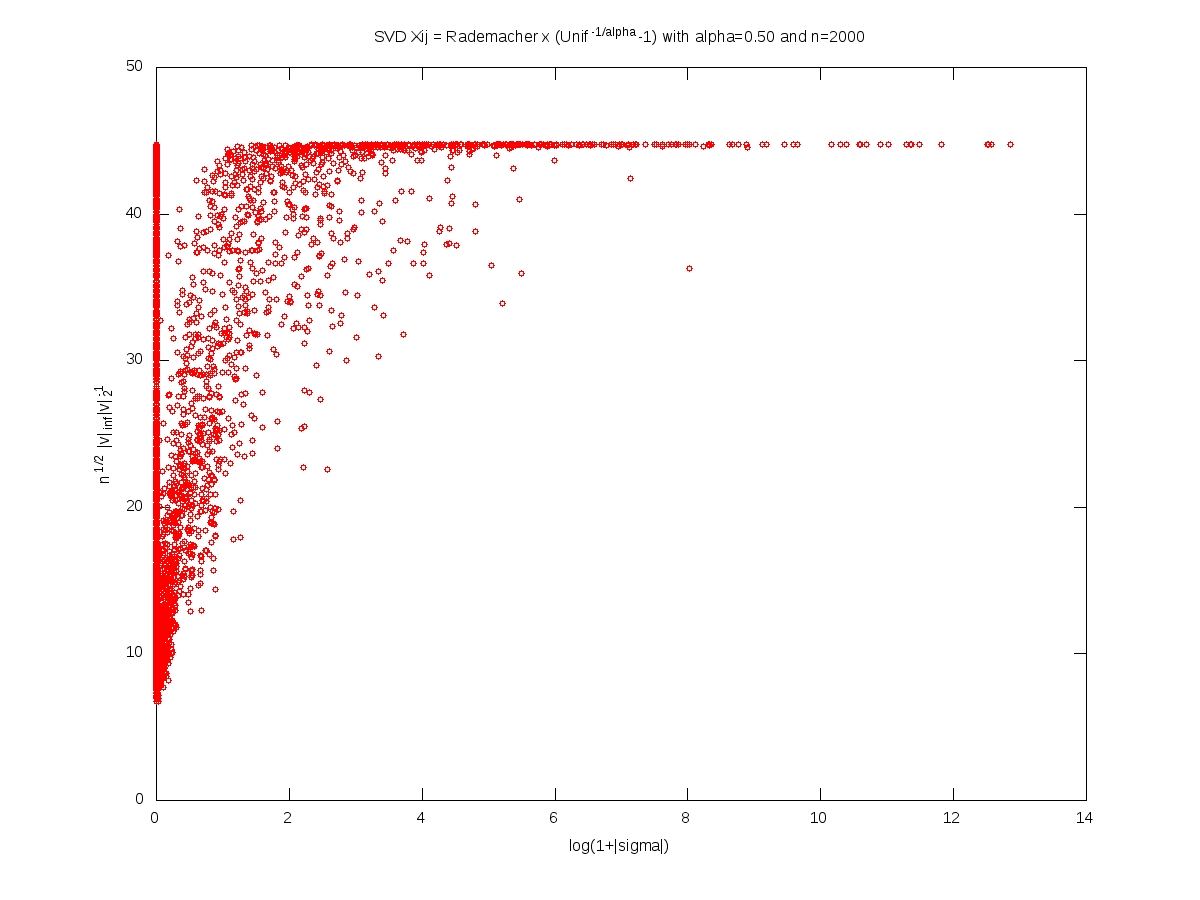
We measure the localization of an eigenvector $v\in\mathbb{R}^n$, $v\neq0$, by the norm ratio $\sqrt{n}\left\Vert v\right\Vert_\infty \left\Vert v\right\Vert_2^{-1}$.
In what follows, the matrix $X$ is $n\times n$, with i.i.d. entries and $X_{11}=\varepsilon (U^{-1/\alpha}-1)$ where $\varepsilon$ and $U$ are independent with $\varepsilon$ symmetric Rademacher (random sign) and $U$ uniform on $[0,1]$. For every $t>0$, we have $$\mathbb{P}(|X_{11}|>t)=(1+t)^{-\alpha}.$$
Each of the following plots corresponds to a single realization of the matrix. In each plot, each small red cirlce corresponds to a couple (eigenvalue, eigenvector). A logarithmic scale is used for the eigenvalues, while the localization is used for the eigenvectors. The notion of ``bulk of the spectrum'' is unclear when $\alpha<2$. Beware that we should not 100% trust numerics when dealing with heavy tailed random matrices (no truncation here).
Symmetric model: eigenvectors localization versus eigenvalues (Octave code)
Full iid model: eigenvectors localization versus singular values (Octave code)
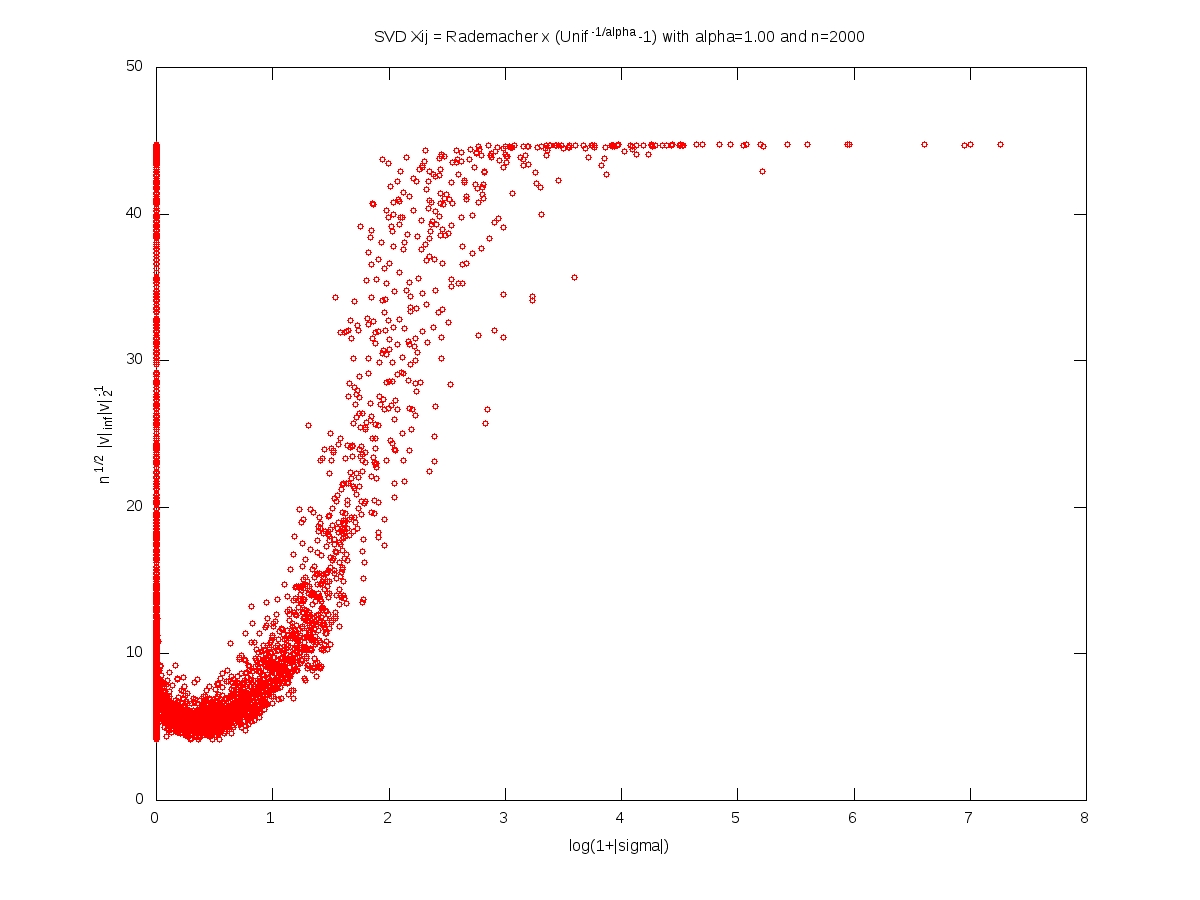
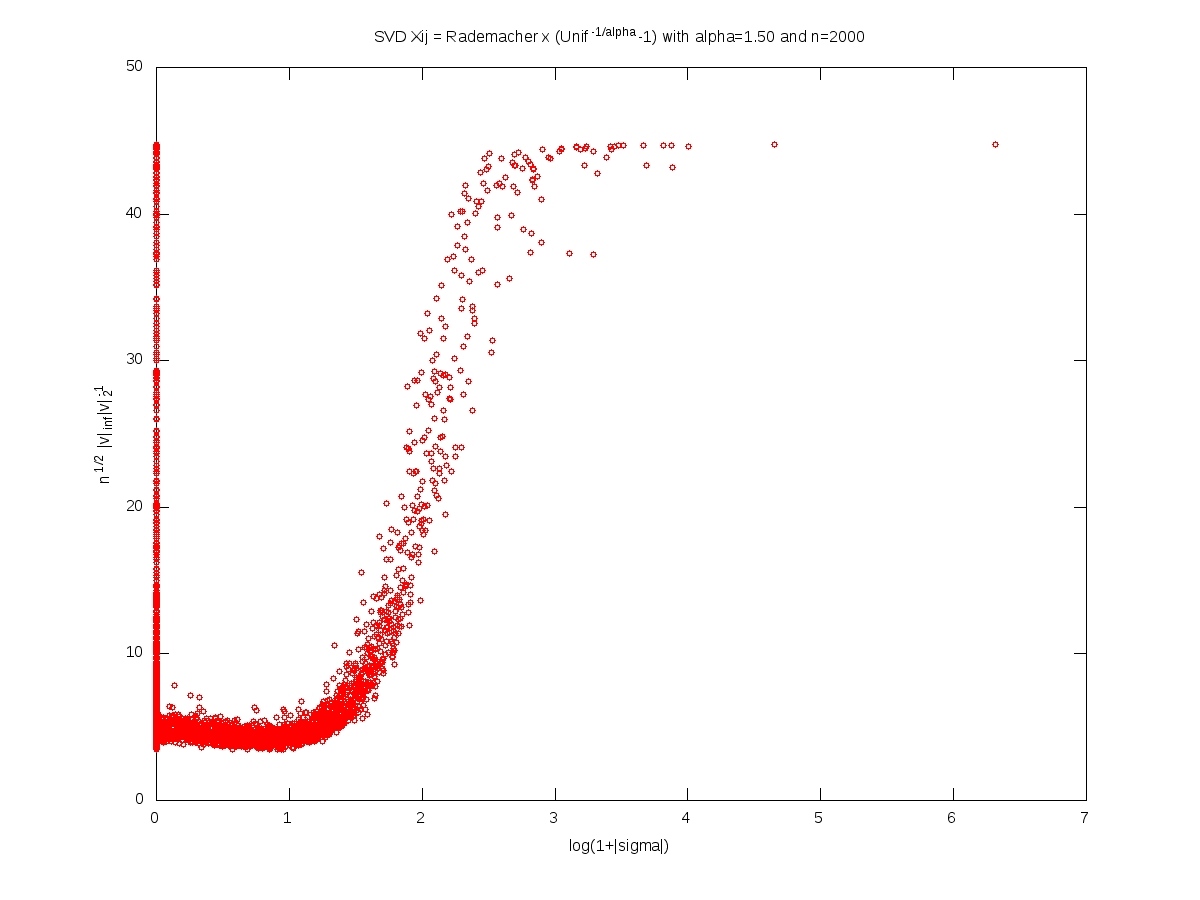
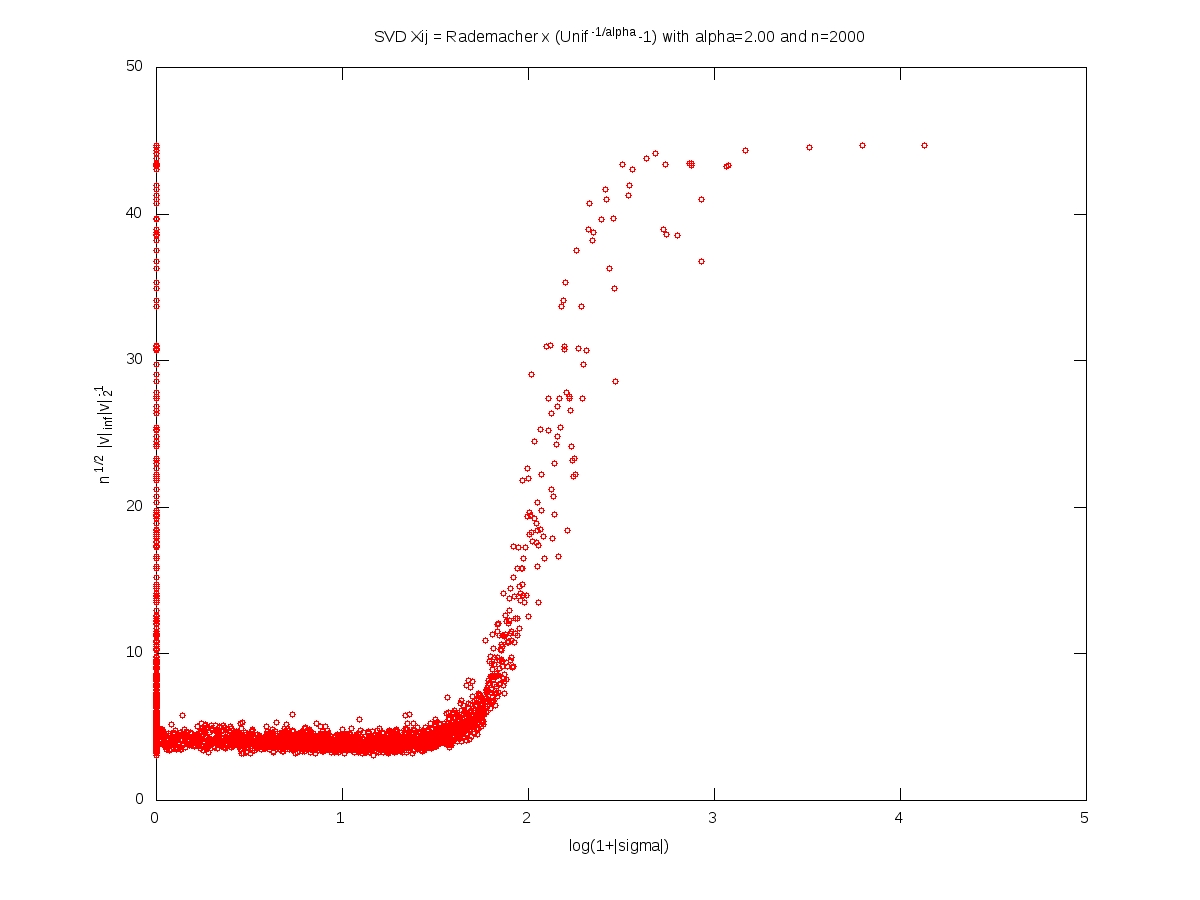
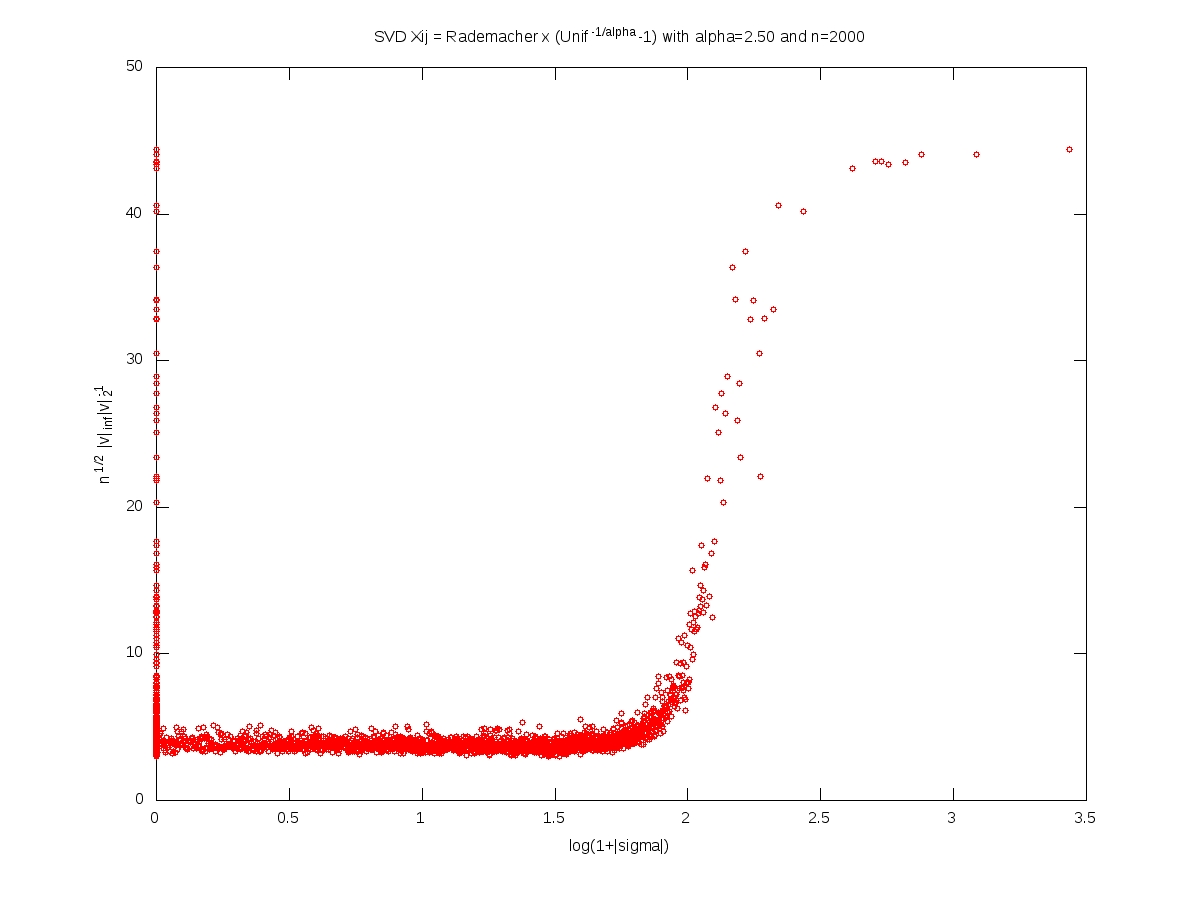
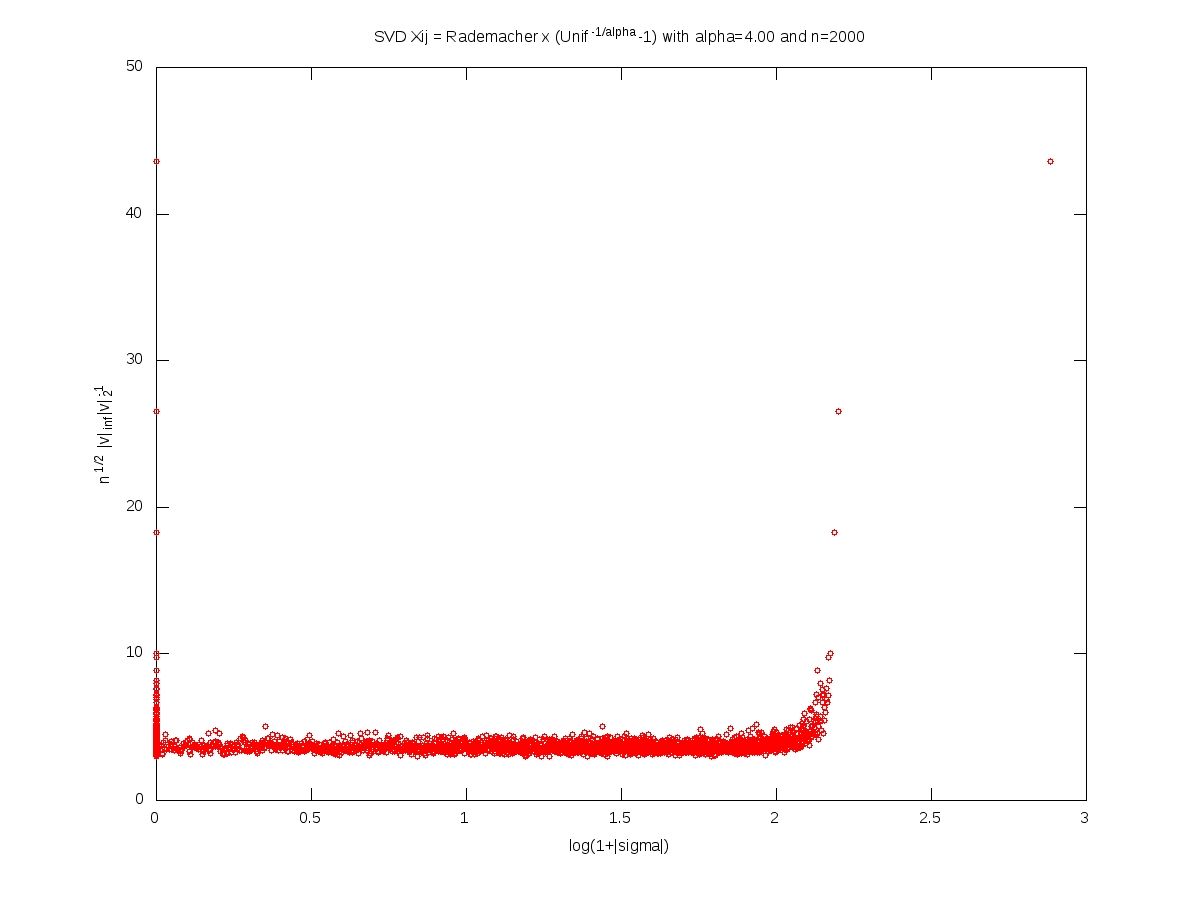
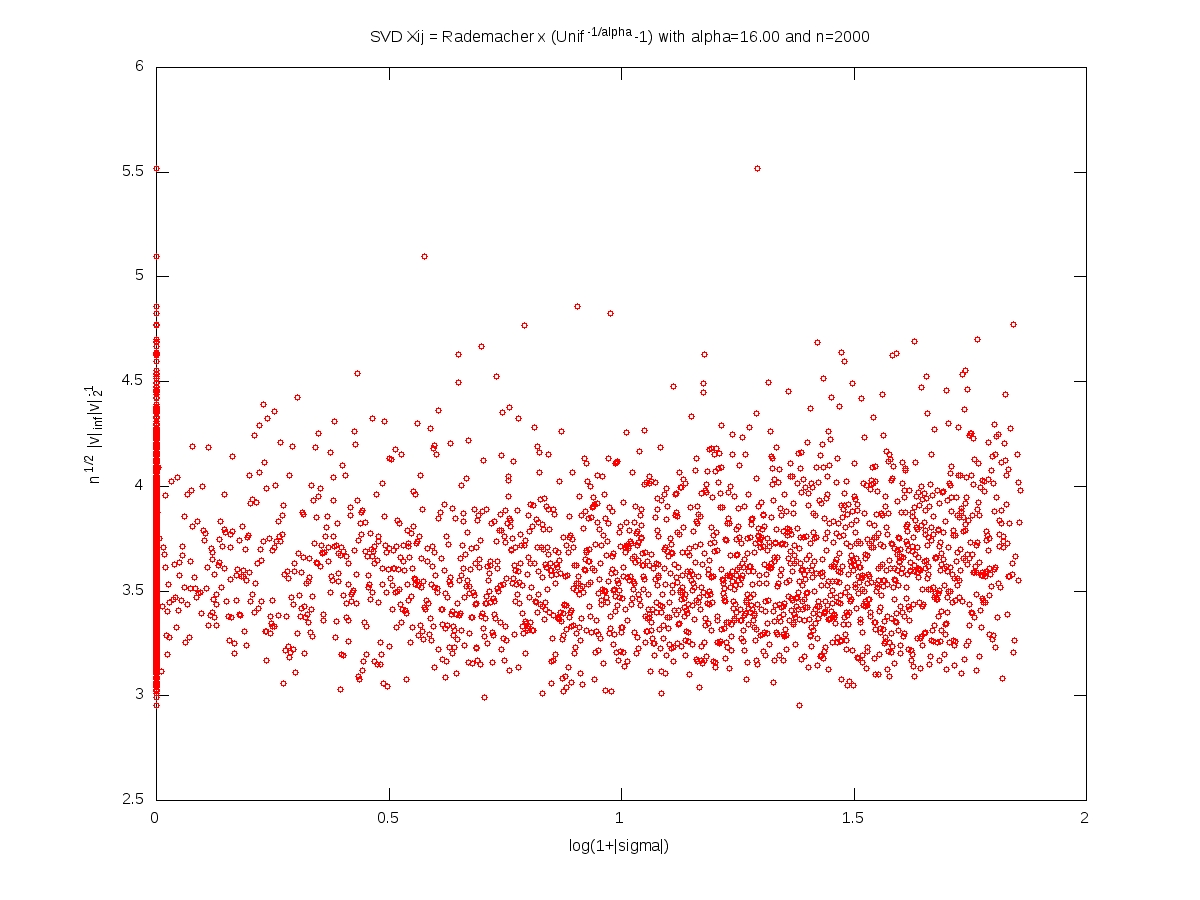
Note: This post is motivated by an animated coffee break discussion with Alice Guionnet and Charles Bordenave during a conference on random matrices (Paris, June 1-4, 2010). You may forge numerous conjectures from these computer simulations. Another interesting problem is the limiting behavior of the eigenvalues or singular values spacings when the dimension goes to infinity, and its dependency over the tail index $\alpha$.
Recent addition to this post: Sandrine Péché pointed out that conjectures have been made by the physicists Bouchaud and Cizeau in their paper Theory of Lévy matrices published in Phys. Rev. E 50, 1810–1822 (1994).
1 Comment