Ce billet est une version longue et en français d'un billet précédent publié en anglais au printemps dernier. Il s'agit d'une contribution au livre collectif pluridisciplinaire « Covid-19 : regards croisés sur la crise » en cours de préparation à l'université Paris-Dauphine. Le texte fait un peu plus de 10 000 caractères et le résumé environ 1000 caractères, espaces compris.
Résumé. La pandémie de coronavirus actuelle et sa gestion sont des sujets d'étude intéressants à bien des égards. Si l'on se penche sur l'histoire récente et moins récente, cette pandémie en elle-même apparaît pour l'instant comme plutôt ordinaire, alors que les réponses politiques le sont moins. On observe en particulier, au-delà de l'aversion au risque et d’un mimétisme international, un certain rôle joué par l'analyse quantitative de risque pour la décision, basée sur la modélisation en épidémiologie. Ce texte regroupe des libres pensées sur ce qu’est la modélisation mathématique ou informatique, ce qu’elle n’est pas, le rôle qu’elle a, qu’elle a eu, et qu’elle pourrait avoir. Le propos est d’apporter un contrepoint critique et historique aux tentations utilitaristes qui sous-tendent la modélisation et l’analyse quantitative, exacerbées par la crise du coronavirus que nous vivons.
-
La modélisation mathématique réussit remarquablement à prédire, avec un haut degré de précision, le comportement de nombreux phénomènes naturels, comme par exemple, et très concrètement, la trajectoire des satellites ou la propagation du son et de la lumière. La modélisation mathématique joue indéniablement un rôle clé dans la plupart des champs technologiques actuels, souvent à travers la physique et l’informatique. Ses nombreux succès ont un impact considérable, concret et positif, sur notre vie quotidienne. Comment expliquer un tel succès de la mathématisation du monde ? Quelle est la nature du lien entre mathématiques et monde physique ? Ces questions occupent les penseurs depuis l’antiquité. Les plus grands esprits s’y attardent, comme le prix Nobel de physique Eugene Wigner, et son célèbre « The unreasonable effectiveness of mathematics in the natural sciences » publié en 1960, ou le grand mathématicien et informaticien Richard Hamming, et son « The unreasonable effectiveness of mathematics » publié en 1980. Sans vraiment apporter de réponse sur le fond, ces articles dessinent les contours d’une fascinante réussite, qui passe par une quantification et une mécanisation des phénomènes naturels.
D’un autre côté, il se trouve que les mécanismes de nombreux phénomènes naturels quantifiables ne sont pas bien compris, et même lorsqu'ils sont bien compris à une certaine échelle, leur modélisation mathématique n’est en général qu’une approximation parfois grossière de leur complexité et subtilité, qui peut beaucoup manquer de précision. L'approximation peut également provenir de l'analyse mathématique et numérique du modèle en lui-même, ainsi que du manque de données pour l'ajuster. Tous ces aspects sont bien connus des mathématiciens, qui ont coutume de dire que tous les modèles sont faux, mais que certains sont utiles. Ces limitations de la modélisation mathématique des phénomènes naturels, liées au caractère simpliste voire caricatural de la mathématisation et numérisation du monde, font contrepoint. L’ingénieur Derek Abbott a publié en 2013 un article remarqué sur ce sujet, intitulé « The reasonable ineffectiveness of mathematics », une sorte de pied de nez à l’arrogance de ceux d’Eugène Wigner et Richard Hamming.
Le cas de la météorologie est particulièrement intéressant. Les mécanismes des phénomènes naturels sous-jacents sont relativement bien compris et sont modélisés mathématiquement notamment par les équations de la mécanique des fluides, liées à l'une des plus grandes questions de physique mathématique. Malheureusement, la sensibilité de ces équations aux perturbations rend la prédiction relativement limitée, malgré les progrès remarquables réalisés dans l'analyse numérique et la puissance de calcul, et malgré l'énorme quantité de données collectées par télédétection par satellite. Les prévisions météorologiques à moyen/long terme restent inaccessibles.
La situation est pire encore pour les sciences sociales comme l'économie ou la sociologie, pour lesquelles nous n'avons pas l'analogue des équations de la mécanique des fluides. Historiquement, l'analyse quantitative des phénomènes sociaux a d'abord été abordée à l'aide de données statistiques, notamment par Adolphe Quetelet, qui a produit entre autres études son célèbre « Sur l'homme et le développement de ses facultés, ou Essai de physique sociale » (1835). Quetelet a découvert une mécanique, une régularité des phénomènes aléatoires, ouvrant la voie à la modélisation mathématique des systèmes désordonnés et à leur prévisibilité. L’idée fondamentale est que ce sont les distributions statistiques ou les lois de probabilités qui sont justiciables d’une mécanique et d’une prédiction, et non pas les phénomènes aléatoires au niveau individuel. Cette distinction entre comportement microscopique ou individuel et comportement macroscopique ou de population pose également le problème philosophique du libre arbitre. Adolphe Quetelet, héritier de Pierre-Simon de Laplace, n'était pas le seul scientifique du dix-neuvième siècle à explorer une vision mécaniste de la nature, les plus célèbres étant peut-être Charles Darwin et Ludwig Boltzmann, dont les idées révolutionnaires ont été longtemps fort controversées avant d’être intégrées dans le corpus scientifique. La mécanisation des systèmes désordonnés amorcée à l’époque a conduit aux grands succès de la théorie des probabilités et de la statistique que nous connaissons tous aujourd’hui, qui sont également au cœur de la physique statistique, de la mécanique quantique, et de la théorie de l'information. Mais les sciences sociales restent malgré tout bien trop complexes pour de nombreux aspects. Les limitations de la modélisation pour l’économie mais aussi la difficulté de l’analyse des données sont abordées par exemple par Thomas Piketty dans « Le Capital au XXIe siècle » (Seuil, 2013).
Le formidable développement de la numérisation, des ordinateurs, des bases de données massives, et des réseaux a conduit à une utilisation généralisée de la modélisation et des algorithmes, bien au-delà des périmètres habituels. Cela a également stimulé le développement de divers types d'apprentissage automatique, produisant des succès parfois étonnants dont on ne comprend pas forcément les tenants et les aboutissants. Ce type de traitement algorithmique des données est toujours considéré comme de la modélisation mais peut différer de la modélisation habituelle en ce qu'il peut produire des prédictions empiriques sans compréhension.
Qu’en est-il de l'épidémiologie ? Il s'avère que les mécanismes biologiques et médicaux des épidémies virales ne sont pas bien compris par les scientifiques pour l'instant, même si la science progresse à l’occasion de chaque épidémie. La modélisation mathématique ou informatique développée en épidémiologie incorpore au mieux ce qui est connu. Elle reste cependant limitée pour la prédiction, et le problème ne se réduit pas à la collecte de données, à la sensibilité des modèles, ou à la complexité des phénomènes. En particulier, cela produit une analyse des risques discutable pour la prise de décision. On pourrait alternativement utiliser les statistiques historiques des épidémies pour produire des prédictions, au moins de nature qualitative ou phénoménologique, mais cela est également relativement limité. Nous sommes donc condamnés à vivre pour l'instant avec d'importantes incertitudes. C'est quelque peu difficile à accepter pour nos sociétés actuelles, dont l’aversion au risque est importante, et dont le rapport à la fin de vie est bouleversé.
La modélisation en épidémiologie n’en demeure pas moins intéressante pour explorer les phénomènes, les hypothèses, faire avancer notre compréhension des mécanismes et de leurs effets. La modélisation permet également la conception d’indicateurs quantitatifs avancés et l’organisation générale des moyens. La controverse fait partie de la science, mais le temps d’élaboration de la science reste cependant bien différent du temps de la décision, du temps politique ou médiatique.
D’autre part, force est de constater qu’en ces temps d’hyperspécialisation, nos scientifiques ne sont plus vraiment philosophes, tandis que nos philosophes ne sont plus vraiment scientifiques. Quant à nos décideurs et à nos journalistes, ils ne sont bien souvent ni l’un ni l’autre. C’est donc aussi de pluridisciplinarité et de pensées croisées, autant à l’échelle individuelle que collective, dont nous avons besoin. Les jeunes esprits y sont réceptifs, et cela peut inspirer et étoffer nos formations universitaires. On a coutume de dire que l’esprit critique et le sens de l’histoire sont essentiels à la science et à sa diffusion. À la fin du seizième siècle, les horoscopes du grand astronome Johannes Kepler, l’un des plus grands scientifiques de tous les temps, étaient très prisés des puissants qui l’employaient, et Kepler lui-même était persuadé que l’astrologie pouvait devenir une science au même titre que l’astronomie. Certaines des prédictions astrologiques de Kepler se sont révélées exactes. L’aventure scientifique depuis cette époque incite les scientifiques à la prudence et à l’humilité, à ne pas devenir de simples marchands de certitudes au service des puissants. Servir des scénarios issus de modélisations approximatives ne risque-t-il pas d’alimenter la peur ou l’insouciance, de produire des excès regrettables y compris pour la science ?
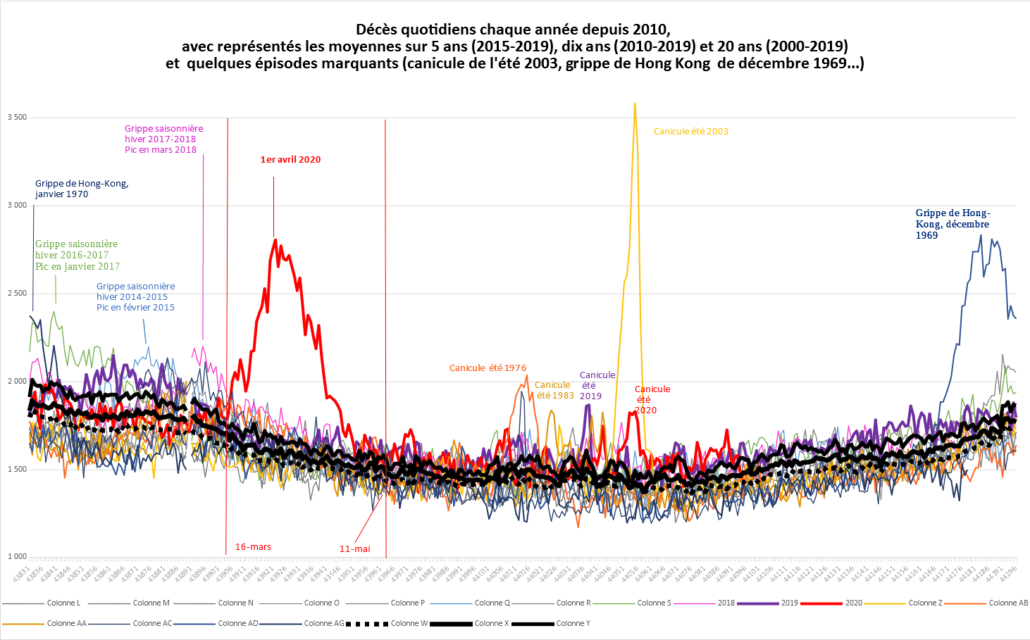
Toujours à propos d’histoire, et concernant la pandémie de coronavirus du printemps 2020 en France, examinons le graphique de l’INSEE qui superpose les courbes de mortalité totale de périodes passées marquantes, notamment la canicule de l’été 2003, des grippes saisonnières des années récentes, et la grippe dite de Hong Kong, qui a frappé la France à l’hiver 1969-1970 dans une quasi-indifférence générale. La chose la plus frappante est peut-être la similarité en forme et en taille entre le pic de cette grippe de Hong Kong et celui de l’épidémie de coronavirus du printemps 2020. En 2020, un confinement de la population a été organisé, par mimétisme international et au vu des prédictions issues de modélisations en épidémiologie. Comment en évaluer l’efficacité globale et la pertinence ? La démarche scientifique est assez limitée car il n’est pas possible de répéter l’expérience en contrôlant les paramètres. L’effet sur les accidents de la route, souvent évoqué, est bien réel mais une simple règle de trois révèle que cela ne change pas énormément les choses quantitativement. La médecine a certainement évolué entre les deux époques. D’autre part, la population française en 1969-1970 était bien plus petite et bien plus jeune qu’en 2020. L’essentiel des décès en question concerne les personnes âgées, pour partie en établissement spécialisé. Notons également que la grippe dite espagnole en fin de première guerre mondiale – absente du graphique – a plutôt tué les jeunes adultes, par surinfection bactérienne, avant l’ère des antibiotiques. Tout cela souligne aussi bien la tentation et la difficulté à comparer à travers le temps. Une analyse du même type pourrait aussi être menée à travers l’espace. Ces phénomènes extrêmes et récurrents sont encore plus complexes et hétérogènes que les crues des fleuves dont les bassins évoluent. Il s’agit là d’un problème majeur de l’analyse de données à travers le temps et l’espace. La principale difficulté à laquelle est confronté Thomas Piketty dans son travail sur le capital est précisément l’hétérogénéité spatio-temporelle des données statistiques concernant l’économie.