Aspects of the Heisenberg group

The Heisenberg group is a remarkable simple mathematical object, with interesting algebraic, geometric, and probabilistic aspects. It is available in tow flavors: discrete and continuous. The (continuous) Heisenberg group \( {\mathbb{H}} \) is formed by the real \( {3\times 3} \) matrices of the form

\[ \begin{pmatrix} 1 & x & z \\ 0 & 1 & y \\ 0 & 0 & 1 \\ \end{pmatrix}, \quad x,y,z\in\mathbb{R}. \]

The Heisenberg group is a non-commutative sub-group of \( {\mathrm{GL}_3(\mathbb{R})} \):

\[ \begin{pmatrix} 1 & x & z \\ 0 & 1 & y \\ 0 & 0 & 1 \\ \end{pmatrix} \begin{pmatrix} 1 & x’ & z’ \\ 0 & 1 & y’ \\ 0 & 0 & 1 \\ \end{pmatrix} = \begin{pmatrix} 1 & x+x’ & z+z’+xy’ \\ 0 & 1 & y+y’ \\ 0 & 0 & 1 \\ \end{pmatrix} \]

The inverse is given by

\[ \begin{pmatrix} 1 & x & z \\ 0 & 1 & y \\ 0 & 0 & 1 \\ \end{pmatrix}^{-1} = \begin{pmatrix} 1 & -x & -z+xy \\ 0 & 1 & -y \\ 0 & 0 & 1 \\ \end{pmatrix}. \]

(the discrete Heisenberg group is the discrete sub-group of \( {\mathbb{H}} \) formed by the elements of \( {\mathbb{H}} \) with integer coordinates). The Heisenberg group \( {\mathbb{H}} \) is a Lie group. Its Lie algebra \( {\mathfrak{H}} \) is the sub-algebra of \( {\mathcal{M}_3(\mathbb{R})} \) given by the \( {3\times 3} \) real matrices of the form

\[ \begin{pmatrix} 0 & a & c \\ 0 & 0 & b \\ 0 & 0 & 0 \\ \end{pmatrix}, \quad a,b,c\in\mathbb{R} \]

The exponential map \( {\exp:A\in\mathcal{L}\mapsto\exp(A)\in\mathbb{H}} \) is a diffeomorphism. This allows to identify the group \( {\mathbb{H}} \) with the algebra \( {\mathfrak{H}} \). Let us define

\[ X= \begin{pmatrix} 0 & 1 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{pmatrix}, \quad Y= \begin{pmatrix} 0 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \\ \end{pmatrix}, \quad\text{and}\quad Z= \begin{pmatrix} 0 & 0 & 1 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{pmatrix}. \]

We have then

\[ [X,Y]=XY-YX=Z\quad\text{and}\quad [X,Z]=[Y,Z]=0. \]

The Lie algebra \( {\mathfrak{H}} \) is nilpotent of order \( {2} \):

\[ \mathfrak{H}=\mathrm{span}(X,Y)\oplus\mathrm{span}(Z). \]

This makes the Baker-Campbell-Hausdorff formula on \( {\mathfrak{H}} \) particularly simple:

\[ \exp(A)\exp(B)=\exp\left(A+B+\frac{1}{2}[A,B]\right). \]

The names Heisenberg group and Heisenberg algebra come from the fact that in quantum physics, and following Werner Heisenberg and Hermann Weyl, the algebra generated by the position operator and the momentum operator is exactly \( {\mathfrak{H}} \). The identification of \( {\mathbb{H}} \) with \( {\mathfrak{H}} \)

\[ \begin{pmatrix} 1 & a & c \\ 0 & 1 & b \\ 0 & 0 & 1 \\ \end{pmatrix} \equiv \exp \begin{pmatrix} 0 & x & z \\ 0 & 0 & y \\ 0 & 0 & 0 \\ \end{pmatrix} =\exp(xX+yY+zZ) \]

allows to identify \( {\mathbb{H}} \) with \( {\mathbb{R}^3} \) equipped with the group structure

\[ (x,y,z)(x’,y’,z’)=(x+x’,y+y’,z+z’+\frac{1}{2}(xy’-yx’)) \]

and

\[ (x,y,z)^{-1}=(-x,-y,-z). \]

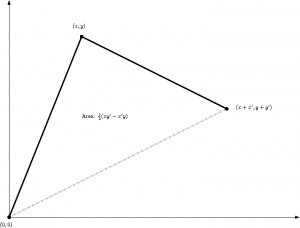
This is the exponential coordinates of \( {\mathbb{H}} \). Geometrically, the quantity \( {\frac{1}{2}(xy’-yx’)} \) is the algebraic area in \( {\mathbb{R}^2} \) between the piecewise linear path

\[ [(0,0),(x,y)]\cup[(x,y),(x+x’,y+y’)] \]

and its chord

\[ [(0,0),(x+x’,y+y’)]. \]

This area is zero if \( {(x,y)} \) and \( {(x’,y’)} \) are colinear. The group product encodes the sum of increments in \( {\mathbb{R}^2} \) and computes automatically the generated area.

The Heisenberg group \( {\mathbb{H}} \) is topologically homeomorphic to \( {\mathbb{R}^3} \) and the Lebesgue measure on \( {\mathbb{R}^3} \) is a Haar measure on \( {\mathbb{H}} \). However, as a manifold, its geometry is sub-Riemannian: the tangent space (at the origin and thus everywhere) is of dimension \( {2} \) instead of \( {3} \), putting a constraint on the geodesics (due to the lack of vertical speed vector, some of them are helices instead of straight lines). The Heisenberg group \( {\mathbb{H}} \) is also a metric space for the so called Carnot-Carathéodory sub-Riemannian distance. The Heisenberg group is a Carnot group. Its Hausdorff dimension with respect to the Carnot-Carathéodory metric is \( {4} \), in contrast with its dimension as a topological manifold which is \( {3} \).

The dilation semigroup of automorphisms \( {(\mathrm{dil}_t)_{t\geq0}} \) on \( {\mathbb{H}} \) is defined by

\[ \mathrm{dil}_t \exp \begin{pmatrix} 0 & x & z \\ 0 & 0 & y \\ 0 & 0 & 0 \\ \end{pmatrix} = \exp \begin{pmatrix} 0 & tx & t^2z \\ 0 & 0 & ty \\ 0 & 0 & 0 \\ \end{pmatrix} . \]

Let \( {(x_n,y_n)_{n\geq0}} \) be the simple random walk on \( {\mathbb{Z}^2} \) starting from the origin. If one embed \( {\mathbb{Z}^2} \) into \( {\mathbb{H}} \) by \( {(x,y)\mapsto xX+yY} \) then one can consider the position at time \( {n} \) in the group by taking the product of increments in the group:

\[ \begin{array}{rcl} S_n=(x_1,y_1)\cdots(x_n,y_n) &=&(s_{n,1},s_{n,2},s_{n,3}) \\ &=&(x_1+\cdots+x_n,y_1+\cdots+y_n,s_{n,3}). \end{array} \]

These increments are commutative for the first two coordinates (called the horizontal coordinates) and non commutative for the third coordinate. The first two coordinates of \( {S_n} \) form the position in \( {\mathbb{Z}^2} \) of the random walk while the third coordinate is exactly the algebraic area between the random walk path and its chord on the time interval \( {[0,n]} \). We are now able to state the Central Limit Theorem on the Heisenberg group:

\[ \left(\mathrm{dil}_{1/\sqrt{n}}(S_{\lfloor nt\rfloor})\right)_{t\geq0} \quad \underset{n\rightarrow\infty}{\overset{\text{law}}{\longrightarrow}} \quad \left(B_t,A_t\right)_{t\geq0} \]

where \( {(B_t)_{t\geq0}} \) is a simple Brownian motion on \( {\mathbb{R}^2} \) and where \( {(A_t)_{t\geq0}} \) is its Lévy area (algebraic area between the Brownian path and its chord, seen as a stochastic integral). The stochastic process \( {(\mathbb{B}_t)_{t\geq0}=((B_t,A_t))_{t\geq0}} \) is the sub-Riemannian Brownian motion on \( {\mathbb{H}} \).

\[ \begin{array}{rcl} \mathbb{B}_t &=& (B_t,A_t) \\ &=&(B_{t,1},B_{t,2},A_t) \\ &=& \exp \begin{pmatrix} 0 & B_{t,1} & \frac{1}{2}\left(\int_0^t\!B_{s,1}dB_{s,2}-\int_0^t\!B_{t,2}dB_{t,1}\right) \\ 0 & 0 & B_{t,2} \\ 0 & 0 & 0 \end{pmatrix} \\ &=& \begin{pmatrix} 1 & B_{t,1} & \int_0^t\!B_{s,1}dB_{s,2} \\ 0 &1 & B_{t,2} \\ 0 &0 &1 \end{pmatrix}. \end{array} \]

The process \( {(\mathbb{B}_t)_{t\geq0}} \) has independent and stationary (non-commutative) increments and belong the class of Lévy processes, associated to (non-commutative) convolution semigroups on \( {\mathbb{H}} \). The law of \( {\mathbb{B}_t} \) is infinitely divisible and maybe seen as a sort of Gaussian measure on \( {\mathbb{H}} \). The process \( {(\mathbb{B}_t)_{t\geq0}} \) is also a Markov diffusion process on \( {\mathbb{R}^3} \) admitting the Lebesgue measure as an invariant reversible measure, and with infinitesimal generator

\[ L=\frac{1}{2}(V_1^2+V_2^2)=\frac{1}{2}\left((\partial_x-\frac{1}{2}y\partial_z)^2+(\partial_y+\frac{1}{2}x\partial_z)^2\right). \]

We have \( {V_3:=[V_1,V_2]=\partial_z} \) and \( {[V_1,V_3]=[V_2,V_3]=0} \). The linear differential operator \( {L} \) on \( {\mathbb{R}^3} \) is hypoelliptic but is not elliptic. It is called the sub-Laplacian on \( {\mathbb{H}} \). A formula for its heat kernel was computed by Lévy using Fourier analysis (it is an oscillatory integral).

Note that \( {L} \) acts like the two dimensional Laplacian on functions depending only on \( {x,y} \). Note also that the Riemannian Laplacian on \( {\mathbb{H}} \) is given by

\[ L+\frac{1}{2}V_3^2=\frac{1}{2}\left(V_1^2+V_2^2+V_3^3\right) =\frac{1}{2}\left((\partial_x-\frac{1}{2}y\partial_z)^2+(\partial_y+\frac{1}{2}x\partial_z)^2+(\partial_z)^2\right). \]

Open question. Use the CLT to obtain a sub-Riemannian Poincaré inequality or even a logarithmic Sobolev inequality on \( {\mathbb{H}} \) for the heat kernel. It is tempting to try to adapt to the sub-Riemannian case the strategy used by L. Gross (for Riemannian Lie groups). This question is naturally connected to my previous work on gradient bounds for the heat kernel on the Heisenberg group, in collaboration with D. Bakry, F. Baudoin, and M. Bonnefont.

Related reading. (among many other references)

• An introduction to the geometry of stochastic flows, by Baudoin
• A tour of subriemannian geometries, their geodesics and applications, by Montgomery
• Probabilities on the Heisenberg group, by Neuenschwander
• An intro. to Lie groups and geometry of homogeneous spaces, by Arvanitoyeorgos
• Metric structures for Riemannian and non-Riemannian spaces, by Gromov
• Moderate growth and random walk on finite groups, by Diaconis and Saloff-Coste