Recently, a friend of mine was asking about the relative strength of probability journals. Beyond sociological aspects, a quantitative answer to such a question is probably a non constant random vector. Even if I do not trust bibliometrics, I like to play with data. The Mathematical Reviews have introduced the concept of Mathematical Citation Quotient (MCQ), a ratio of two counts for a selected journal and a selected year. The MCQ for year $Y$ and journal $J$ is given by the formula $$\mathrm{MCQ}=\frac{m}{n}$$ where
- $m$ is the total number of citations of papers published in jounal $J$ in years $Y-1$,…,$Y-5$ by papers published in year $Y$ in any journal known by MathSciNet;
- $n$ is the total number of papers published in journal $J$ in years $Y-1$,…,$Y-5$.
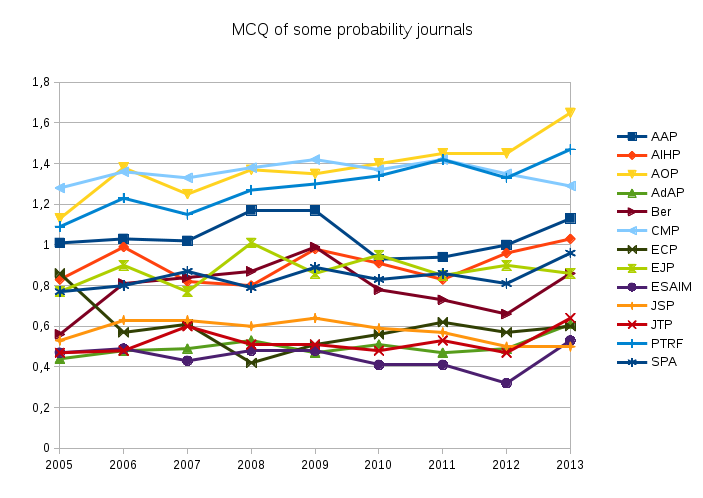
The Mathematical Reviews compute every year the MCQ for every indexed journal, and make it available on MathSciNet. This formula is very similar to the one of the five years impact factor, the main difference being the population of journals which is specifically mathematical for the MCQ (reference list journals). Here is the evolution of the MCQ for few probability journals. The MCQ data was extracted from MathSciNet by a Python program. The graphic was produced with LibreOffice. We see here that there are roughly three groups. It could be exciting to build a stochastic model for such phenomena (self organization and reinforcement). The funny thing is that this blog post contributes to the reinforcement!
Since a citation is a vote, one may think about taking into account the importance of the voter, which leads to a recursive formula and to a fixed point. In this spirit, and if you like Markov chains, you may take a look at eigenfactor, a website providing bibliometrics based on the Markovian approach of Google PageRank. There is also SCImago Journal & Country Rank. You may also read the article by John Ewing entitled Measuring Journals (Notices of the AMS, 2006).