
The social status of journals is, first of all, a way to assign a value to papers without being forced to read them. This seems to be crucial for the social aspects of science : hiring, promotion, funding, ... The Mathematical Citation Quotient, computed by MathSciNet, is a way to quantify the social value of journals, which turns out to be compatible with what people have in mind. We refer to the posts written from 2013 to 2018 (see below) for more information on the MCQ.
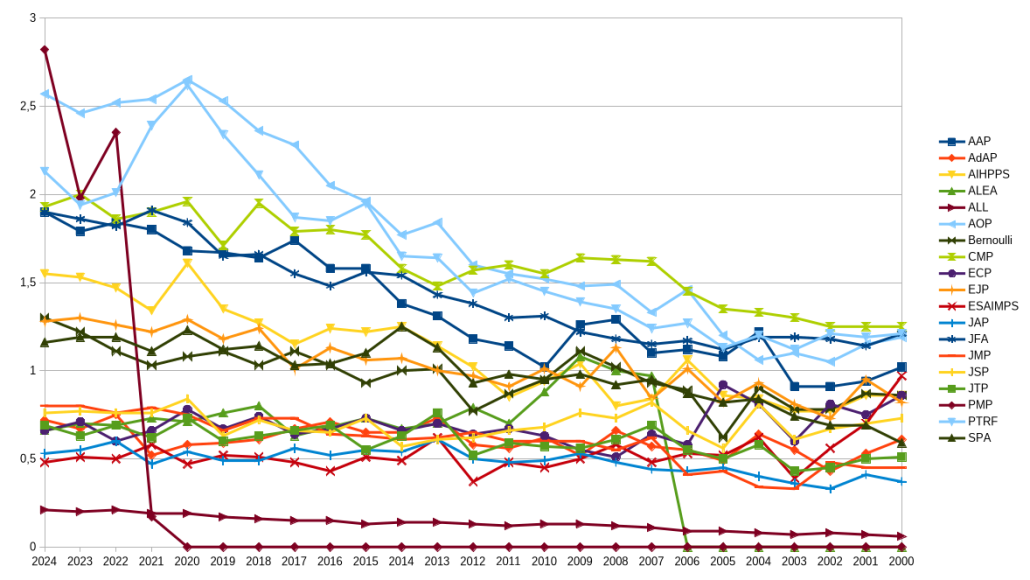
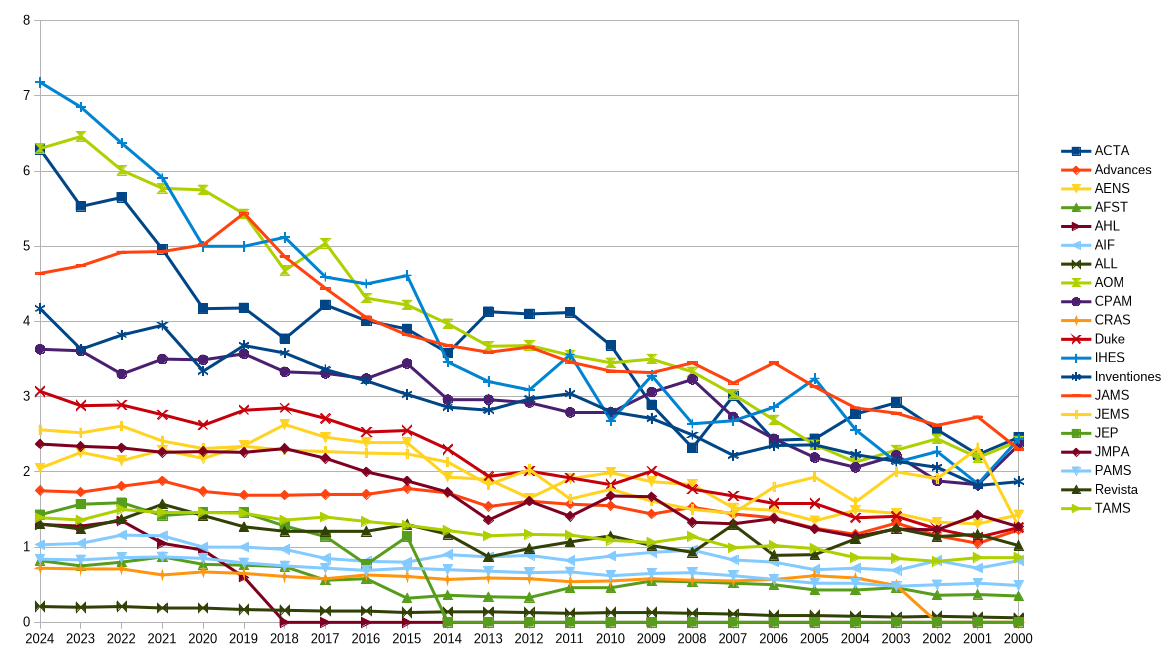
To be honest, since my fifties, I have little interest in the social status of the journal where I publish, and I leave the decision to my co-authors, if any. However, I still find interesting the study of the physics of the social value of journals. It is a dynamic collective phenomenon incorporating reinforcement. Here is the MCQ for a bunch of probability journals, and of generalist journals. We see the special evolution of certain journals, as well as the emergence of categories. In particular, the launch of PMP, a CMP killer, seems to be a success, so far.
Further reading on this blog.
Leave a Comment