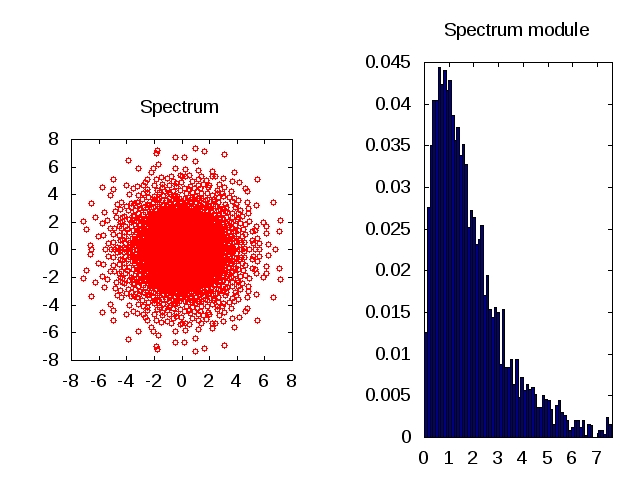
I have recently uploaded the paper arXiv:1006.1713 [math.PR] entitled Spectrum of non-Hermitian heavy tailed random matrices, written in collaboration with Charles Bordenave and Pietro Caputo.
We provide a rigorous analysis of the phenomenon behind the pictures above. Let \( {(X_{jk})_{j,k\geq1}} \) be i.i.d. complex random variables with cumulative distribution function \( {F} \). Our main result is a heavy tailed counterpart of Girko's circular law when \( {F} \) has an infinite second moment. Roughly, if \( {F} \) is in the attraction domain of an \( {\alpha} \)-stable law, with \( {0<\alpha<2} \), then we prove that there exist a deterministic sequence \( {a_n\sim n^{1/\alpha}} \) and a probability measure \( {\mu_\alpha} \) on \( {\mathbb{C}} \) depending only on \( {\alpha} \) such that with probability one, the empirical distribution of the eigenvalues of the rescaled matrix \( {(a_n^{-1}X_{jk})_{1\leq j,k\leq n}} \) converges weakly to \( {\mu_\alpha} \) as \( {n\rightarrow\infty} \). Our approach combines Aldous & Steele's objective method with Girko's Hermitization using logarithmic potentials. The underlying limiting object is defined on a bipartized version of Aldous' Poisson Weighted Infinite Tree. Recursive relations on the tree provide some properties of \( {\mu_\alpha} \). In contrast with the Hermitian and Hermitized cases, we find that \( {\mu_\alpha} \) is not heavy tailed.
Let us first recall that the eigenvalues of an \( {n\times n} \) complex matrix \( {M} \) are the roots in \( {\mathbb{C}} \) of its characteristic polynomial. We label them \( {\lambda_1(M),\ldots,\lambda_n(M)} \) with non growing modules and growing phases. We also denote by \( {s_1(M)\geq\cdots\geq s_n(M)} \) the singular values of \( {M} \), defined for every \( {1\leq k\leq n} \) by \( {s_k(M):=\lambda_k(\sqrt{MM^*})} \). We define the empirical spectral measure and the empirical singular values measure as
\[ \mu_M = \frac 1 n \sum_{k=1} ^n \delta_{\lambda_k (M)} \quad \text{and } \quad \nu_M = \frac 1 n \sum_{k=1} ^n \delta_{s_k (M)}. \]
Let us define the \( {n\times n} \) random matrix \( {X = (X_{ij}) _{ 1 \leq i, j \leq n}} \). Following Dozier and Silverstein, if \( {F} \) has finite positive variance \( {\sigma^2} \), then for every \( {z\in\mathbb{C}} \), there exists a probability measure \( {\mathcal{Q}_{\sigma,z}} \) on \( {[0,\infty)} \) depending only on \( {\sigma} \) and \( {z} \), with explicit Cauchy-Stieltjes transform, such that a.s. (almost surely)
\[ \nu_{\frac{1}{\sqrt{n}}X-zI} \underset{n\rightarrow\infty}{\rightsquigarrow} \mathcal{Q}_{\sigma,z} \ \ \ \ \ (1) \]
where \( {\rightsquigarrow} \) denotes the weak convergence of probability measures. The proof of (1) is based on a classical approach for Hermitian random matrices with bounded second moment: truncation, centralization, recursion on the resolvent, and cubic equation for the limiting Cauchy-Stieltjes transform (fixed point characterization). In the special case \( {z=0} \), the statement (1) reduces to the quartercircular law theorem (square version of the Marchenko-Pastur theorem (see e.g. Marchenko and Pastur, Wachter, Yin) and the probability measure \( {Q_{\sigma,0}} \) is the quartercircular law with Lebesgue density
\[ x\mapsto \frac{1}{\pi\sigma^2}\sqrt{4\sigma^2-x^2}\mathbf{1}_{[0,2\sigma]}(x). \ \ \ \ \ (2) \]
Girko's famous circular law theorem states under the same assumptions that a.s.
\[ \mu_{\frac{1}{\sqrt{n}}X} \underset{n\rightarrow\infty}{\rightsquigarrow} \mathcal{U}_\sigma \ \ \ \ \ (3) \]
where \( {\mathcal{U}_\sigma} \) is the uniform law on the disc \( {\{z\in\mathbb{C};|z|\leq\sigma\}} \). This statement was established through a long sequence of partial results Mehta, Girko, Silverstein, Edelman, Girko, Bai, Girko, Bai and Silverstein, Pan and Zhou, Götze and Tikhomirov, Tao and Vu, the general case (3) being finally obtained by Tao and Vu, by using Girko's Hermitization with logarithmic potentials and uniform integrability, the convergence (1), and polynomial bounds on the extremal singular values. The idea of using directly logarithmic potentials was already present in the work of Goldsheid and Khoruzhenko for non-Hermitian random tridiagonal matrices.
The aim of our work is to investigate what happens when \( {F} \) does not have a finite second moment. We shall consider the following hypothesis:
- (H1) there exists a slowly varying function \( {L} \) (i.e. \( {\lim_{t\rightarrow\infty}L(x\,t)/L(t) = 1} \) for any \( {x>0} \)) and a real number \( {\alpha\in(0,2)} \) such that for every \( {t\geq1} \)
\[ \mathbb{P} ( |X_{11}| \geq t ) = \int_{\{z\in\mathbb{C};|z| \geq t\}}\!dF(z) = L(t)t^{-\alpha}, \]
and there exists a probability measure \( {\theta} \) on the unit circle \( {\mathbb{S}^1:=\{z\in\mathbb{C};|z|=1\}} \) of the complex plane such that for every Borel set \( {D\subset \mathbb{S}^1} \),
\[ \lim_{t \rightarrow \infty} \mathbb{P} \left( \frac{X_{11}}{|X_{11}|} \in D \Bigm| |X_{11} | \geq t \right) = \theta(D). \]
Assumption (H1) states a complex version of the classical criterion for the domain of attraction of a real \( {\alpha} \)-stable law, see e.g. theorem IX.8.1a in Feller's book. For instance, if \( {X_{11}=V_1+iV_2} \) with \( {i=\sqrt{-1}} \) and where \( {V_1} \) and \( {V_2} \) are independent real random variables both belonging to the domain of attraction of an \( {\alpha} \)-stable law then (H1) holds. When (H1) holds, we define the sequence
\[ a_n := \inf\{a > 0 \text{ s.t. } n \mathbb{P}(|X_{11}| \geq a) \leq 1\} \]
and (H1) implies that
\[ \lim_{n\rightarrow\infty}n \mathbb{P}(|X_{11}| \geq a_n ) = \lim_{n\rightarrow\infty} n a_n^{-\alpha} L(a_n)=1. \]
It follows then classically that for every \( {n\geq1} \)
\[ a_n = n^{1/\alpha}\ell(n) \]
for some slowly varying function \( {\ell} \). The additional possible assumptions on \( {F} \) to be considered in the sequel are the following:
- (H2) \( {\mathbb{P}(|X_{11}|\geq t) \sim_{t \rightarrow \infty} c\, t^{-\alpha}} \) for some \( {c>0} \) (this implies \( {a_n\sim_{n\rightarrow\infty}c^{1/\alpha}n^{1/\alpha}} \))
- (H3) \( {X_{11}} \) has a bounded probability Lebesgue density on \( {\mathbb{R}} \) or on \( {\mathbb{C}} \).
One can check that (H1-H2-H3) hold e.g. when the module \( {|X_{11}|} \) and the phase \( {X_{11}/|X_{11}|} \) are independent with \( {|X_{11}|=|S|} \) where \( {S} \) is real symmetric \( {\alpha} \)-stable and the phase follows a Dirac mass or an absolutely continuous law. Another basic example is given by \( {X_{11}=\varepsilon W^{-1/\alpha}} \) with \( {\varepsilon} \) and \( {W} \) independent such that \( {\varepsilon} \) takes values in \( {\{-1,1\}} \) and \( {W} \) is uniform on \( {[0,1]} \).
For every \( {n\geq1} \), let us define the i.i.d. \( {n\times n} \) complex matrix \( {A =A_n} \) by
\[ A_{ij} := a_n ^{-1}X_{ij} \ \ \ \ \ (4) \]
for every \( {1\leq i,j\leq n} \). Our first result concerns the singular values of \( {A-zI} \), \( {z\in\mathbb{C}} \).
Theorem 1 (Singular values) If (H1) holds then for all \( {z \in \mathbb{C}} \), there exists a probability measure \( {\nu_{\alpha,z}} \) on \( {[0,\infty)} \) depending only on \( {\alpha} \) and \( {z} \) such that a.s.
\[ \nu_{A-zI} \underset{n\rightarrow\infty}{\rightsquigarrow} \nu_{\alpha,z}. \]
The case \( {z=0} \) was already obtained by Belinschi, Dembo and Guionnet. Theorem 1 is a heavy tailed version of the Dozier and Silverstein theorem (1). Our main results below give a heavy tailed version of Girko's circular law theorem (3), as well as a non-Hermitian version of Wigner's theorem for Lévy matrices considered by Bouchaud and Cizeau, Ben Arous and Guionnet, Belinschi, Dembo and Guionnet, and arXiv:0903.3528 [math.PR].
Theorem 2 (Eigenvalues) If (H1-H2-H3) hold then there exists a probability measure \( {\mu_\alpha} \) on \( {\mathbb{C}} \) depending only on \( {\alpha} \) such that a.s.
\[ \mu_{A} \underset{n\rightarrow\infty}{\rightsquigarrow} \mu_\alpha. \]
Theorem 3 (Limiting law) The probability distribution \( {\mu_\alpha} \) from theorem 2 is isotropic and has a continuous density. Its density at \( {z=0} \) equals
\[ \frac{\Gamma(1+2/\alpha)^2\Gamma(1+\alpha/2)^{2/ \alpha}} {2\pi\Gamma(1-\alpha/2)^{2/\alpha}}. \]
Furthermore, up to a multiplicative constant, the density of \( {\mu_\alpha} \) is equivalent, as \( {\left|z\right|\rightarrow\infty} \), to
\[ |z|^{2 ( \alpha - 1) } e^{- \frac{\alpha}{2} |z|^\alpha}. \]
Recall that for a normal matrix (i.e. which commutes with its adjoint), the module of the eigenvalues are equal to the singular values. Theorem 3 reveals a striking contrast between \( {\mu_\alpha} \) and \( {\nu_{\alpha,0}} \). The limiting law of the eigenvalues \( {\mu_{\alpha}} \) has a stretched exponential tail while the limiting law \( {\nu_{\alpha,0}} \) of the singular values is heavy tailed with power exponent \( {\alpha} \), see e.g. Belinschi, Dembo and Guionnet. This does not contradict the identity
\[ \prod_{k=1}^n|\lambda_k(A)|= \prod_{k=1}^ns_k(A) \]
and the Weyl inequalities but it does indicate that \( {A} \) is typically far from being a normal matrix. A similar shrinking phenomenon appears already in the finite second moment case (1-3): the law of the module under the circular law \( {\mathcal{U}_\sigma} \) has density
\[ r\mapsto 2\sigma^{-2}r\mathbf{1}_{[0,\sigma]}(r) \]
in contrast with the density (2) of the quartercircular law \( {\mathcal{Q}_{\sigma,0}} \) (even the supports differ by a factor \( {2} \)).
The proof of theorem 1 relies on an extension to non-Hermitian matrices of the ``objective method'' approach developed in arXiv:0903.3528 [math.PR]. More precisely, we build an explicit operator on Aldous' Poisson Weighted Infinite Tree (PWIT) and prove that it is the local limit of the matrices \( {A_n} \) in an appropriate sense. While Poisson statistics arises naturally as in all heavy tailed phenomena, the fact that a tree structure appears in the limit is roughly explained by the observation that non vanishing entries of the rescaled matrix \( {A_n=a_n^{-1}X} \) can be viewed as the adjacency matrix of a sparse random graph which locally looks like a tree. In particular, the convergence to PWIT is a weighted-graph version of familiar results on the local structure of Erdös-Rényi random graphs. The method relies on the local weak convergence, a notion introduced by Benjamini and Schramm, Aldous and Steele, see also Aldous and Lyons.
The proof of theorem 2 relies on Girko's Hermitization method with logarithmic potentials, on theorem 1, and on polynomial bounds on the extremal singular values needed to establish a uniform integrability property. This extends the Hermitization method to more general settings, by successfully mixing various arguments already developed in arXiv:0903.3528 [math.PR], arXiv:0808.1502 [math.PR], and by Tao and Vu. Following them, one of the key step will be a lower bound on the distance of a row of the matrix \( {A} \) to a subspace of dimension at most \( {n - n^{1- \gamma}} \), for some small \( {\gamma >0} \). We also use a concentration for empirical spectral distributions in order to obtain the almost sure convergence in the Hermitization.
Girko's Hermitization method gives a characterization of \( {\mu_\alpha} \) in terms of its logarithmic potential. In our settings, however, this is not convenient to derive properties of the measure \( {\mu_\alpha} \), and our proof of theorem 3 is based on an analysis of a self-adjoint operator on the PWIT and a recursive characterization of the spectral measure from the resolvent of this operator. We develop an efficient machinery to analyze the complex spectral measures which avoids a direct use of the logarithmic potential and the singular values. Our approach builds upon similar methods in the physics literature, e.g. Feinberg and Zee, Gudowska-Nowak, Nowak, and Pappe, and Rogers and Castillo. The Cauchy-Stieltjes transform is based on complex numbers and constitutes an efficient tool for the spectral analysis of Hermitian random matrices. Beyond Hermitian random matrices, a quaternionic version of it may be used. However, for non normal random matrices, this does not work. We propose a new approach based on bipartization, in which the quaternions are replaced by suitable \( {2\times 2} \) matrices.
The derivation of a Markovian version of theorems 1 and 2 is an interesting open problem that will be analyzed elsewhere, see arXiv:0903.3528 [math.PR] for the symmetric case and arXiv:0808.1502 [math.PR] for the light tailed non-symmetric case. It is also tempting to seek for an interpretation of \( {\nu_{\alpha,z}} \) and \( {\mu_\alpha} \) in terms of a sort of graphical free probability theory. With a proper notion of trace, it is possible to define the spectral measure of an operator, see e.g. Brown, Haagerup and Schultz, Lyons, but we do not pursue this goal here. The study of localization of eigenvectors of heavy tailed random matrices is also an interesting problem.
Leave a Comment