
This post is about the recent work arXiv:2405.00120 with Ryan Matzke, Edward Saff, Minh Quan Vu, and Robert Womersley. It belongs to classical analysis and potential theory. More precisely, we study Riesz energy problems with radial external fields, on the full Euclidean space. In particular, when the external field is a power of the Euclidean norm, we completely characterize the values of the power for which dimension reduction occurs in the sense that the support of the equilibrium measure becomes a sphere.
Riesz kernel. The Riesz kernel of parameter $s\in(-2,\infty)$ in dimension $d\geq1$ is defined by
\[
K(x):=
\begin{cases}
\displaystyle\frac{1}{s\|x\|^s} & \text{if $s\neq0$}\\[1.5em]
\displaystyle\log\frac{1}{\|x\|} & \text{if $s=0$}
\end{cases},
\] for $x\in\mathbb{R}^d$, $x\neq0$. The special case $s=d-2$ is the Coulomb or Newton kernel.
Riesz energy with external field. For a probability measure $\mu$ on $\mathbb{R}^d$, we define
\[
\mathrm{I}(\mu):=\iint(K(x-y)+V(x)+V(y))\mathrm{d}\mu(x)\mathrm{d}\mu(y).
\] We focus on the situation where the external field $V$ is a power :
\[
V(x):=\frac{\gamma}{\alpha}\|x\|^\alpha,\quad\gamma>0,\ \alpha>\max(-s,0).
\]
Equilibrium measure. The functional $\mathrm{I}$ is strictly convex, and there exists a unique probability measure $\mu$, called the equilibrium measure, denoted $\mu_{\mathrm{eq}}$, such that
\[
\mathrm{I}(\mu_{\mathrm{eq}})=\min_{\mu}\mathrm{I}(\mu)<\infty.
\] It is radially symmetric and has compact support.
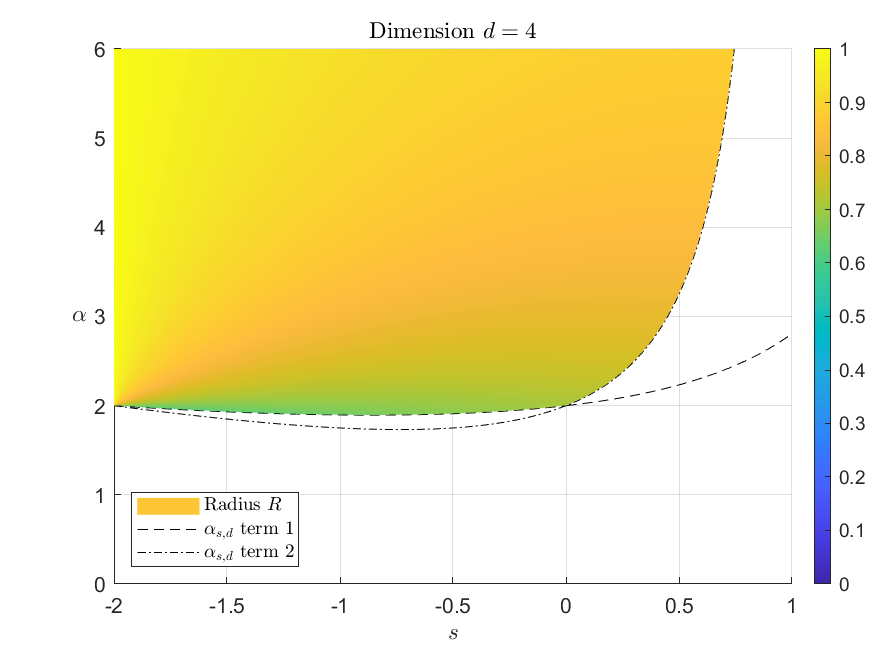
Threshold phenomenon. Let $\sigma_R$ be the uniform probability measure on the sphere of radius $R$. Our main discovery is that if $s\in(-2,d-3)$ then there exists a critical value $\alpha_*$ such that
\[
\mu_{\mathrm{eq}}=\sigma_R\text{ for some }R\quad\text{ if and only if }\quad\alpha\geq\alpha_*.
\] Moreover $\alpha_*$ and $R$ are explicit functions of $(s,d)$ and $(s,d,\alpha)$ respectively :
\begin{align*}
\alpha_*
&= \max\left\{ \dfrac{sc}{2-2c}, \ 2- \dfrac{(s+2)(d-s-4)}{2(d-s-3)}\right\}\\
R
&= \left( \frac{c}{2 \gamma} \right)^{\frac{1}{\alpha + s}}
= \left( \frac{\Gamma(\frac{d}{2}) \Gamma(d-s-1)}{ 2 \gamma \Gamma( \frac{d-s}{2}) \Gamma(d – \frac{s}{2}-1)}
\right)^{\frac{1}{\alpha + s}}
\end{align*} where $c := {}_2\mathrm{F}_1\Bigr(\frac{s}{2}, \frac{2+s-d}{2}; \frac{d}{2}; 1\Bigr)%
=\frac{\Gamma(\frac{d}{2})\Gamma(d -s-1)}
{\Gamma(\frac{d-s}{2})\Gamma(d-\frac{s}{2}-1)}$. The proof involves the Frostman characterization, the Funk-Hecke formula, the calculus of hypergeometric functions, and some black magic.
The active bound in $\alpha_*$ changes at $s=d-4$, for which $\alpha_*=2$. The properties of $c$ ensure that $\alpha_*\geq\max(-s,0)$ and $\alpha_*$ is continuous at $s=0$. More is in arXiv:2405.00120.
Riesz brothers. Frigyes Riesz (1880 — 1956) and Marcell Riesz (1886 — 1969) were brothers. Frigyes is one of the founders of functional analysis, and Alfréd Rényi was one of his doctoral students. Marcell is one of the developpers of potential theory and harmonic analysis among other fields, Harald Cramér, Otto Frostman, Lars Hörmander, and Olof Thorin were one of his doctoral students. The Riesz brothers have a unique joint work, on analytic measures.
Marcel Riesz was born in Györ, Hungary, November 16, 1886 and died in Lund, Sweden, on September 4, 1969. He studied in Budapest, Göttingen and Paris. In 1911 Mittag-Leffler invited him to come to Sweden where he taught at Stockholms Högskola. In 1926 he was appointed professor of mathematics at the university of Lund. After retiring from this position in 1952 he went to the United States where he was visiting research professor at the universities of Maryland and Chicago and other places. He returned to Lund in 1962.
…
Marcel Riesz was the youngest member of a generation of brilliant Hungarian mathematicians that included among others Leopold Fejér, Riesz’s elder brother Frederick Riesz and Alfred Haar. His first paper (1906) is an exposition in Hungarian of a subject of current interest at the time, namely various summation methods for Taylor series of analytic functions. One of these methods, due to Mittag-Leffler, sums the series in a starshaped region bounded by singular points, the Mittag-Leffler star. Common interest in these matters was the beginning of the association with Mittag-Leffler. They seem to have met for the first time in Stockholm in 1908.
…
Riesz’s work after he moved to Lund marks a break with the past. He acquired new interests, starting work in potential theory and wave propagation including Dirac’s equation of the electron and relativity theory. He also took a continuing interest in elementary number theory. His most important contributions are in potential theory and wave propagation. In both cases he invented new multi-dimensional analogues of the Riemann-Liouville integral.
…
Riesz wrote clearly and well and paid much attention to form. His favourite language was French and his style, steeped in the classical tradition, sometimes borders on the precious. Mathematical research always involves competition for fame and a place in the hierarchy, but he made it seem a gentleman’s game. He was of course no stranger to ambition and had to assert himself both in Sweden and in the cosmopolitan world he came from. He admired his illustrious brother Frederick and they had cordial relations. They wrote one paper together, but otherwise there is a clear distance in content between their work, perhaps a result of a conscious effort on Marcel’s part. Seen together they had much physical resemblance but very different temperaments, Frederick calm with great poise and Marcel quick and restless in comparison. Marcel Riesz knew an astonishing number of mathematicians and over the years made and kept many friends among them.
…
Mittag-Leffler had made Stockholms Högskola a center of mathematical research. It had a peak of activity before and around the turn of the century and its other mathematicians, Bendixson, von Koch and Fredholm were famous names. Some ten years later, however, their scientific activity was on the wane for various reasons. Riesz filled a mathematical vacuum. He learnt Swedish quickly and he was very active in the local mathematical society where he soon became the dominating figure. He was lively, accessible, an enthusiastic teacher and a good lecturer with a thorough knowledge of his field. His charming expository lecture from 1913, written in Swedish, has a distinct personal touch reflecting these qualities. In 1923, Riesz lost a competition for a chair in Lund to Carleman. Shortly afterwards von Koch died and Bendixson, Fredholm and Phragmén made a move to appoint Riesz as von Koch’s successor. The move failed and the call went to Carleman. Shortly afterwards, Riesz got a position in Lund. At least in the beginning, he must have felt his stay in Lund as an exile. He had been very successful in Stockholm where, among others, Harald Cramér and Einar Hille had been his personal students.Lund did not have much of a mathematical tradition but Riesz’s arrival meant a change of atmosphere. He was now an international star, active with his own research and he also had the time and incentive to broaden his interests. Frostman’s thesis was a success and there were others after him. Lars Hörmander was one of Riesz’s last personal students in Sweden. Riesz’s work on fractional potentials was the origin of the contributions from Lund to the theory of partial differential operators.
…
Excerpt from Marcel Riesz in memoriam by Lars Gårding, in Acta Math. 124 (1970)
…Lars Gårding invited me to spend three days in Lund, one of the best mathematics departments in Sweden. He initiated me to the very important work of the Soviet mathematieian Petrowski; “Petrowski is my God, and I am his prophet,” he said laughing. I returned to Lund several times later on, and in 1981 I was awarded a doctorate honoris causa there. I had many conversations with Lars Gårding, a devotee of distributions, and with Marcel Riesz. Marcel and Frederic Riesz were two remarkable Hungarian mathematicians: Frederic was tall and thin, Marcel small and fat (Laurel and Hardy). Frederic lived in Hungary, but Marcel was in Lund. He discovered results on partial differential equations, in particular the solution of hyperbolic equations of non-integral order, via symbolic calculation on Hadamard’s finite parts. This problem was adapted to the use of distributions, so he was interested in my talks. Marcel Riesz was a solid drinker, occasionally pushing the limits. One night, we stayed in his house until two in the morning, with a glass of liquor in front of each of us. His glass kept refilling itself. I didn’t touch mine, so every time he looked at it, he saw it was full and thought I had served myself. Later he told Gårding that I was an “excellent drinker” . I remained very close to them. When Riesz came to dinner at our house, we served a chocolate cake, decorated with the wave equation written in white cream – he was enchanted! The young Lars Hörmander was at that time still in high school. Some years later, this future Fields Medalist, trained by Gårding, stood out at the university and became one of the world specialists in partial differential equations. He profited indirectly from my stay, because he made extensive use of distributions. We also became close friends.
…
Excerpt from A Mathematician Grappling with His Century, Birkhäuser 2001, by Laurent Schwartz. This last excerpt was suggested to me by my old friend Arnaud Guyader.
Further reading on this blog.
- Mellin transform and Riesz potentials
2022-08-26 - Unexpected phenomena for equilibrium measures
2022-06-27 - The Funk-Hecke formula
2021-05-22 - Equilibrium measures and obstacle problems
2022-12-11