Circular law theorem for random Markov matrices

I have uploaded on arXiv a paper written with Charles Bordenave and Pietro Caputo entitled Circular Law Theorem for Random Markov Matrices. We provide, probably for the first time, an almost sure  circular law theorem for a model of random matrices with dependent entries and finite positive variance. This work leads us to formulate some open problems of variable difficulty, listed at the end of the introduction. Feel free to solve them!

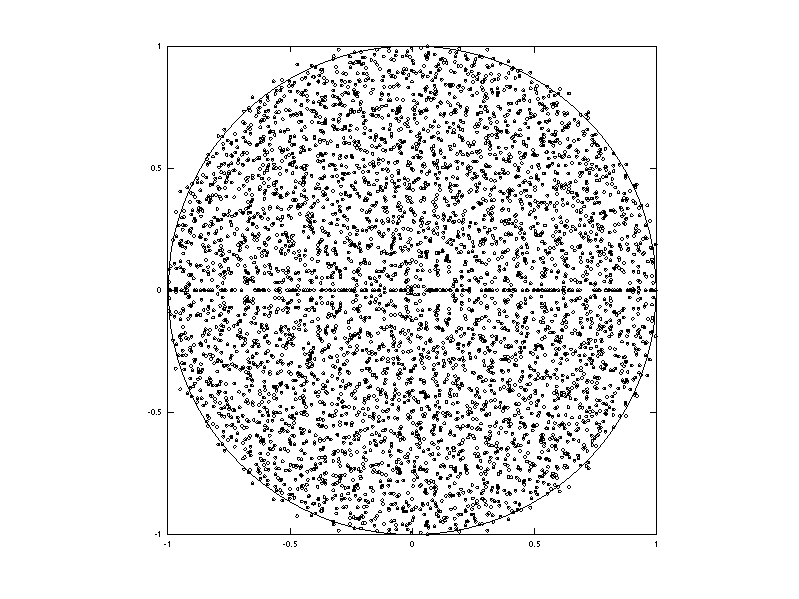
To be a bit more precise, let $(X_{jk})_{jk\geq1}$ be i.i.d. nonnegative random variables with bounded density, mean $m$, and finite positive variance $\sigma^2$. Let $M$ be the $n\times n$ random Markov matrix with i.i.d. rows defined by $M_{jk}=X_{jk}/(X_{j1}+\cdots+X_{jn})$.  Let $\lambda_1,\ldots,\lambda_n$ be the eigenvalues of $\sqrt{n}M$ i.e. the roots in $\mathbb{C}$ of its characteristic polynomial. Our main result states that with probability one, the counting probability measure $\frac{1}{n}\delta_{\lambda_1}+\cdots+\frac{1}{n}\delta_{\lambda_n}$ converges weakly as $n\to\infty$ to the uniform law on the disk $\{z\in\mathbb{C}:|z|\leq m^{-1}\sigma\}$ (circular law).

In particular, when $X_{11}$ follows an exponential law, the random matrix $M$ belongs to the Dirichlet Markov Ensemble of random stochastic matrices, and our main result gives a positive answer to the question raised in a previous paper.

The matrix $M$ is Markov: its entries belong to $[0,1]$ and each row sums up to $1$. It has equally distributed dependent entries. However, the rows of $M$ are i.i.d. and follow an exchangeable law on $\mathbb{R}^n$ supported by the simplex. Since $\sigma<\infty$, the uniform law of large numbers of Bai and Yin states that almost surely

$\displaystyle\max_{1\leq i\leq n}\left|X_{i1}+\cdots+X_{in}-nm\right|=o(n)$.

This suggests that $m^{-1}\sqrt{n}M$ is approximately equal to $n^{-1/2}X$ for $n$ large enough. One can then expect that almost surely the counting probability measure of the singular values of $\sqrt{n}M$ will converge as $n\to\infty$ to  a quartercircular law while the counting probability measure of the eigenvalues of $\sqrt{n}M$ will converges to a circular law. We show that this heuristics is valid. There is however a complexity gap between these two statements due to the fact that for nonnormal operators such as $M$, the eigenvalues are less stable than the singular values under perturbations (here the least singular value enters the scene).

The proof of the main result is inspired from the Tao and Vu version of the Girko Hermitization via logarithmic potentials. More precisely, the starting point is the following Hermitization identity valid for any $n\times n$ complex matrix $A$ and any $z$ outside the spectrum of $A$:

$$\displaystyle \frac{1}{n}\sum_{k=1}^n\log|\lambda_k(A)-z|=\frac{1}{n}\sum_{k=1}^n\log(\lambda_k(\sqrt{(A-zI)(A-zI)^*})).$$

The left hand side is the logarithmic potential at point $z$ of the counting probability measure of the eigenvalues of $A$. The right hand side is the integral of $\log(\cdot)$ for the counting probability measure of the singular values of $A-zI$. Thanks to the Girko Hermitization theorem, the problem boils down then to show that for Lebesgue almost all $z\in\mathbb{C}$, almost surely,

1. the counting probability measure $\nu_{\sqrt{n}M-zI}$ of the singular values of $\sqrt{n}M-zI$ tends weakly as $n\to\infty$ to a deterministic probability measure $\nu_z$ related to the circular law
2. the function $\log(\cdot)$ is uniformly integrable for the sequence $(\nu_{\sqrt{n}M-zI})_{n\geq1}$

For the first statement, we use a result of Dozier and Silverstein, which is based on Hermitian techniques: truncation, centralization,  recursion for the Cauchy-Stieltjes transform (trace of the resolvent) via Sherman-Morrison bloc inversion, producing finally a cubic equation for the Cauchy-Stieltjes transform of the limiting law.

The second statement  involves as essential ingredients a Talagrand concentration inequality (for the control of the distance of rows to the span of other rows), and a polynomial control of the operator norm of the resolvent (i.e. the least singular value of $\sqrt{n}M-zI$). The bounded density assumption is purely technical and comes from the way we control the operator norm of the resolvent. A possible route for the removal of this assumption is to control the least singular value for a certain kind of matrices with independent rows.