The COVID-19 pandemic is an interesting subject of study from many perspectives. Looking back at recent and less recent history, this pandemic by itself appears for now as rather ordinary, while the political responses are truly exceptional. In particular and among several aspects, we can observe, beyond the risk aversion and the international mimetism, a certain role played by risk analysis for decision making based on mathematical modeling for epidemiology.
Mathematical modeling is remarkably successful to predict, with a high degree of accuracy, the behavior of many natural phenomena, such as for example, and very concretely, the trajectory of satellites or the propagation of sound and light. The numerous successes of mathematical modeling have enormous positive concrete impact on our world and our daily life. Around these topics, there is for instance a famous article by Eugene Wigner entitled The Unreasonable Effectiveness of Mathematics in the Natural Sciences (1960), and another one by Richard Hamming entitled The unreasonable effectiveness of mathematics (1980).
On the other hand, the mechanisms of many natural phenomena are not well understood, and even when they are well understood at a certain scale, their mathematical modeling is often an approximation of their complexity and subtleties, which is not always accurate. Approximation may also come from the mathematical and numerical analysis of the model by itself, as well as from the lack of data to fit the model. All these aspects are well known by every mathematician, and it is customary to say that all models are wrong, but some are useful. This reminds on this topic the article entitled The Reasonable Ineffectiveness of Mathematics (2013) by Derek Abbott, pointing out some of the limitations of mathematization.
The case of meteorology is particularly interesting. The mechanisms of the natural phenomenon are relatively well understood and are modeled mathematically by the equations of fluid mechanics, related to one of the greatest questions of mathematical physics. Unfortunately, the sensitivity of these equations to perturbations make the prediction relatively limited, despite the striking progresses made in numerical analysis and computational power, and the enormous amount of data collected by satellite remote sensing. Weather forecasting remains difficult.
The situation is even worse for the social sciences such as economics or sociology, for which we do not have the analogue of the equations of fluid mechanics. Historically, the quantitative analysis of social phenomena were first approached by using statistics, notably by Adolphe Quetelet, who produced among other studies his famous Sur l'homme et le développement de ses facultés, ou Essai de physique sociale (1835). Quetelet discovered some of the mechanical sides of disordered phenomena, paving the way to the mathematical modeling of disordered systems and their predictability. He was not the only scientist to explore the mechanical view of nature at that time, the famous others include certainly Charles Darwin and Ludwig Boltzmann. The mechanization of disordered systems led to the great successes of probability and statistics that we all know, which are also at the heart of statistical physics, quantum mechanics, and information theory. But the social sciences remain too complex for many aspects. This is well explained for instance for economics in Le Capital au XXIe siècle (2013) by Thomas Piketty.
The tremendous development of digitization, computers, and networks has led to the widespread use of mathematical modeling and numerical experiments. It has also stimulated the development of various types of machine learning, producing striking concrete successes. This type of algorithmic data processing is still considered as modeling but may differ from usual modeling in that it can produce empirical prediction without understanding.
How about epidemiology? It turns out that the mechanisms of viral epidemics are not well understood by the scientists for now. The available mathematical or computational modeling incorporates what is known. It remains limited for prediction, and the problem does not reduce to data collection. In particular it produces questionable risk analysis for decision making. We could alternatively use the historical statistics of epidemics to produce predictions, at least at the qualitative or phenomenological level, but this is also relatively limited. We are thus condemned to live for now with important uncertainties. This is somewhat difficult to accept for our present societies.
About the author. Mainly a mathematician, professor at Université Paris-Dauphine - PSL since 2013, presently active in probability theory, mathematical analysis, and statistical physics. Also strongly interested in computer science. Served in the past as a research engineer on data assimilation for the Météo-France research center (one year), researcher in mathematics and signal processing for University of Oxford (one year), researcher in biostatistics and modeling for INRAE (six years), professor of mathematics at Université Paris-Est Marne-la-Vallée (four years), and part-time professor at École Polytechnique (six years). Serves presently as a vice-president in charge of digital strategy for Université Paris-Dauphine for the period 2017-2020.
Further reading on this blog.
- Mathématiques de l'aléatoire et physique statistique (2018), on this blog
- Mathématiques, probabilités, algorithmes (2016), on this blog
- From Boltzmann to random matrices and beyond (2014), for mathematicians, on this blog
- Fondamental et appliqué (2010), on this blog
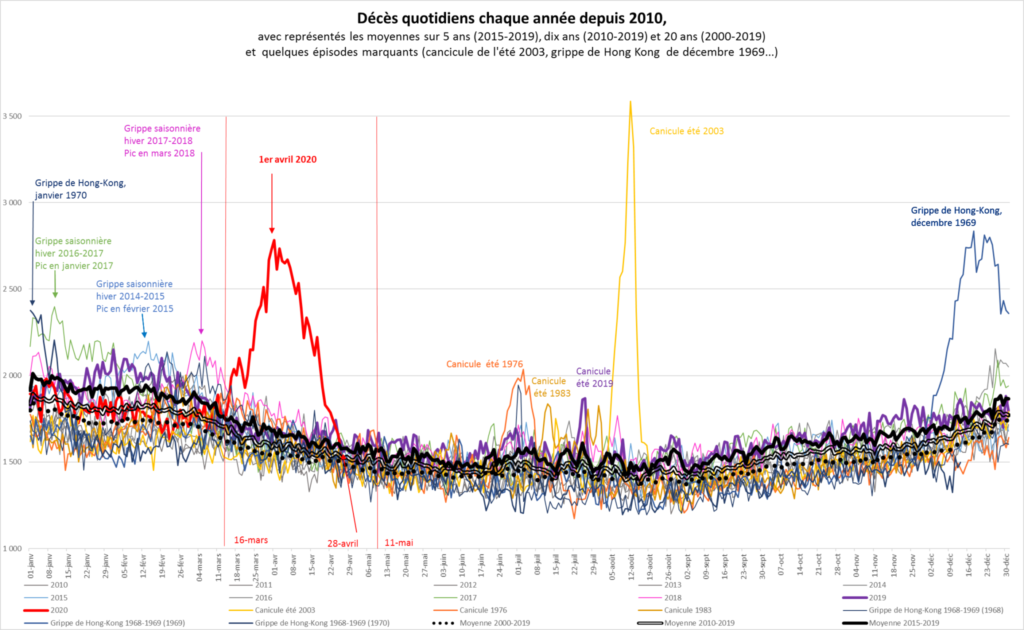
France. Concernant COVID-19 en France, voici un graphique intéressant de l'INSEE, permettant de comparer la mortalité avec quelques éléments du passé, notamment la canicule de l'été 2003, et la grippe de Hong Hong d'il y a cinquante ans. Le confinement est une différence importante. Cependant, on ne sait pas ce qu'aurait donné COVID-19 sans confinement, peut-être un pic plus élevé et moins étalé dans le temps, peut-être pas. Il se peut très bien que le confinement tel qu'il a été organisé n'ait servi à rien voire ait aggravé la situation dans certaines familles et collectivités. L'effet sur les accidents de la route est bien réel mais ne change pas énormément les choses. Une autre différence avec la grippe de Hong Kong est la taille de la population, bien plus petite à l'époque, ainsi que la pyramide des âges, bien plus jeune à l'époque, l'essentiel des décès de la COVID-19 concernant les personnes âgées, pour une bonne part en Ehpad. Notons également que la grippe espagnole en fin de première guerre mondiale - absente du graphique - a plutôt tué les jeunes adultes, par surinfection bactérienne, avant l'ère des antibiotiques. Tout cela souligne la difficulté à comparer à travers le temps. Ces phénomènes extrêmes et récurrents sont encore plus complexes et hétérogènes que les crues des fleuves dont les bassins évoluent. Il s'agit là d'un problème majeur de l'analyse de données à travers le temps et l'espace. La principale difficulté à laquelle est confronté Thomas Piketty dans son travail sur le capital est précisément l'hétérogénéité spatio-temporelle des données statistiques concernant l'économie.
- Le graphique ci-dessous est tiré du billet Statistiques sur les décès : le mode d’emploi des données de l’Insee en 7 questions/réponses publié sur le Blog de l'INSEE.