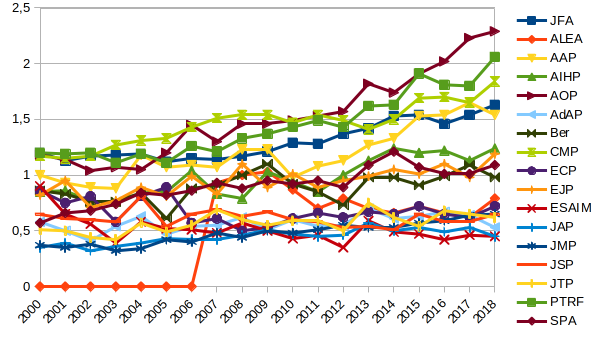
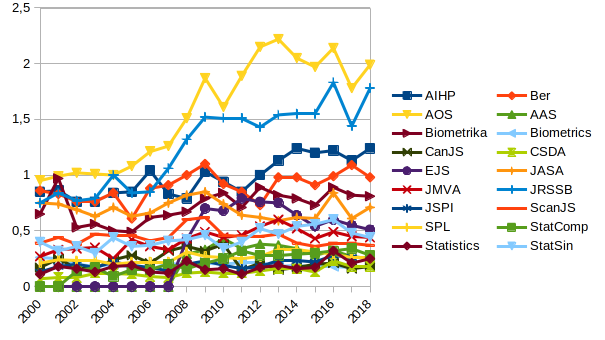
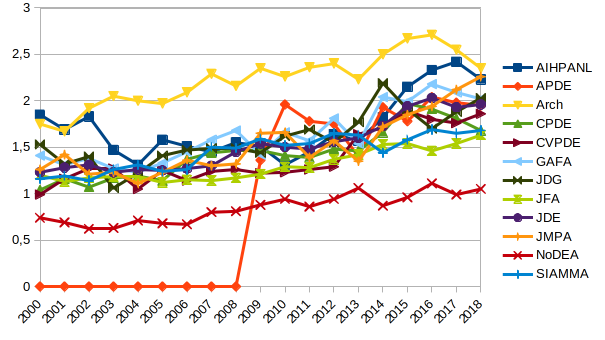
This post gives below the Mathematical Citation Quotient (MCQ) from 2000 to 2018 for journals in probability, statistics, analysis, and general mathematics. The numbers were obtained using home brewed scripts and MathSciNet data. The graphics were created with LibreOffice.
Recall that the MCQ is a ratio of two counts for a selected journal and a selected year. The MCQ for year $Y$ and journal $J$ is given by the formula $\mathrm{MCQ}=m/n$ where
- $m$ is the total number of citations of papers published in jounal $J$ in years $Y-1$,…,$Y-5$ by papers published in year $Y$ in any journal known by MathSciNet;
- $n$ is the total number of papers published in journal $J$ in years $Y-1$,…,$Y-5$.
The Mathematical Reviews compute every year the MCQ for every indexed journal, and make it available on MathSciNet. This formula is very similar to the one of the five years impact factor, the main difference being the population of journals which is specifically mathematical for the MCQ (reference list journals) and the way the citations are extracted. Both biases are negative.
The MCQ is a rough measurement of the social scientific value of journals. The results are quite compatible with what we have in mind. The trends are sometimes intriguing. For probability journals, for instance, it seems that there are three groups. This reminds reinforcement or self-organized criticality. The first group is AOP-PTRF-CMP-JFA-AAP, with some hesitations and an “Annals” naming effect. The second group is AIHP-EJP-SPA-Bernoulli, the third group is ALEA-ECP-AdAP-JAP-JTP-ESAIM. We observe some transitions from one group to another, for instance, since 2010, AAP moved to the first group while ALEA moved to the third group. The case of ECP is very special since its papers are half the standard size. The MCQ probably underestimates the social value of ECP by a rough factor 2, which is logical if we compare with EJP.
Yes, there are more robust ways to measure the social value of a journal, such as for instance the (recursive) eigenfactor, and it could be interesting to check if the three groups are stable!
Leave a Comment