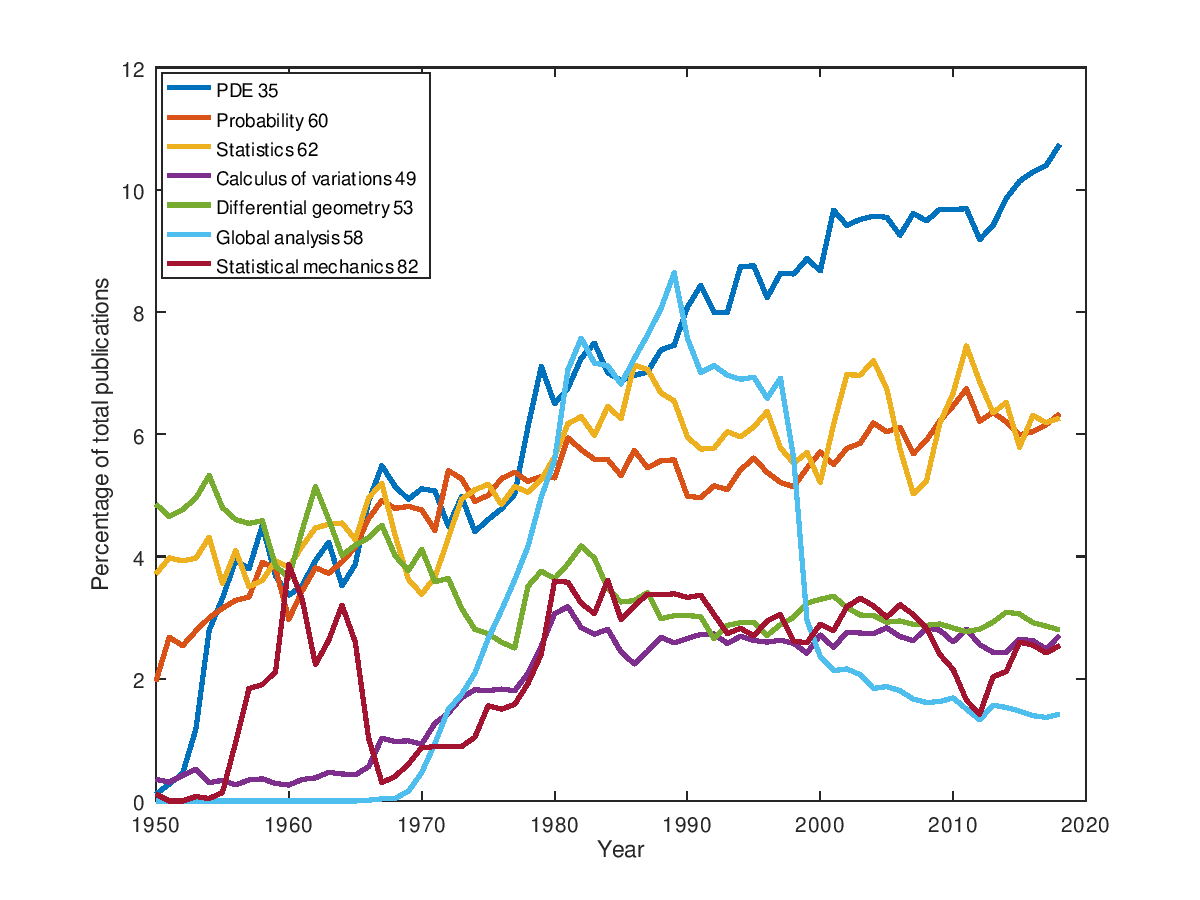
Each journal article in MathSciNet is tagged with one or more MSC classification numbers. Here are the graphics for few of them around analysis, probability, and statistics (this is not exclusive since an article can contain multiple numbers).
Same kind of graphics with more data (beware that the colors are not the same):
Leave a Comment