Concentration for Coulomb gases

This post is about a joint work arXiv:1610.00980 in collaboration with Adrien Hardy and Mylène Maïda. We study the non-asymptotic behavior of Coulomb gases in dimension \( {d\geq2} \). Such gases are modeled by an exchangeable Boltzmann-Gibbs measure with a singular two-body interaction. We obtain concentration of measure inequalities for the empirical distribution of such gases around their equilibrium measure, with respect to bounded Lipschitz and Wasserstein distances. This implies macroscopic as well as mesoscopic convergence in such distances. In particular, we improve the concentration inequalities known for the empirical spectral distribution of Ginibre random matrices. Our work is inspired by the one of Mylène Maïda and Édouard Maurel-Segala (2014) for one-dimensional log-gases, itself inspired by large deviations techniques. Our approach is remarkably simple and bypasses the use of renormalized energy. It involves new inequalities between probability metrics, including Coulomb transport inequalities which can be of independent interest. It allows to recover, extend, and simplify previous results by Nicolas Rougerie and Sylvia Serfaty (2016).

We stress that transportation distances play here a very marginal role in the concentration phenomenon of the empirical measure for Coulomb gases around the equilibrium measure, except if we decide to measure distance with transportation of course. The method is indeed more related to large deviations techniques and comparison of (pseudo)-metrics or divergences. The only deep link is the fact that the Coulomb distance can be compared to a dual Sobolev norm which can be compared in turn to the \( {\mathrm{W}_1} \) metric. This is slightly confusing since on the other hand it is known that transportation distances play a crucial role for the characterization of sub-Gaussian concentration for Lipschitz deformations of Boltzmann-Gibbs measures!

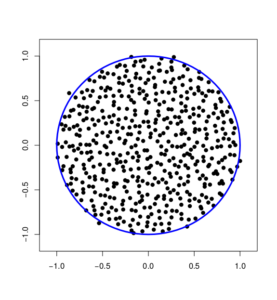
Motivation. Our main motivation is the remakable concentration of measure phenomenon which holds for the complex Ginibre ensemble: if you sample a square random matrix in high dimension with independent and identically distributed complex Gaussian entries of mean zero and variance one then the empirical measure of the eigenvalues of this random matrix will be very close to the uniform distribution on a centered disc with radius equal to the square root of the dimension. It turns out that the law of the eigenvalues of this model of random matrices is a non-product Boltzmann-Gibbs measure: a Coulomb gas or one-component plasma in which the particles are confined and repell each other. This fact suggests to study more generally the concentration of measure phenomenon for Coulomb gases.

Electrostatics. Coulomb kernel in mathematical physics.

Coulomb kernel in \( {\mathbb{R}^d} \), \( {d\geq2} \),
\[ x\in\mathbb{R}^d\mapsto g(x)= \begin{cases} \log\frac{1}{|x|} & \mbox{ if } d=2,\\ \frac{1}{|x|^{d-2}} & \mbox{ if } d\geq3 \end{cases} \]
Fundamental solution of Poisson’s equation
\[ \Delta g=-c_d\, \delta_0 \quad\text{where}\quad c_d = \begin{cases} 2\pi & \mbox{ if } d=2,\\ (d-2)|\mathbb{S}^{d-1}| & \mbox{ if } d\geq3. \end{cases} \]

Coulomb energy and equilibrium measure.

Coulomb energy of probability measure \( {\mu} \) on \( {\mathbb{R}^d} \):
\[ \mathcal{E}(\mu)=\iint g(x-y)\mu(\mathrm{d} x)\mu(\mathrm{d} y)\in \mathbb{R}\cup\{+\infty\}. \]
Coulomb energy with confining potential (external field)
\[ \mathcal{E}_V(\mu)= \mathcal{E}(\mu)+\int V(x)\mu(\mathrm{d} x). \]
Equilibrium probability measure (electrostatics)
\[ \mu_V=\arg\inf\mathcal{E}_V \]
If \( {V} \) is stronger than log at \( {\infty} \) then \( {\mu_V} \) is compactly supported with density
\[ \frac{\Delta V}{2c_d} \]

Examples of equilibrium measures

\[ \begin{array}{c|c|c|c} d & g & V & \mu_V \\\hline\hline 1 & 2 & \infty\mathbf{1}_{\text{interval}^c}(x) & \text{arcsine} \\ 1 & 2 & x^2 & \text{semicircle} \\ 2 & 2 & |x|^2 & \text{uniform on a disc}\\ \geq 3 & d & \Vert x\Vert^2 & \text{uniform on a ball}\\ \geq 2 & d & \text{radial} & \text{radial in a ring} \end{array} \]

Coulomb gas model or one component plasma.

Energy of \( {N} \) Coulomb charges \( {x_1,\ldots,x_N} \) in \( {\mathbb{R}^d} \):
\[ \begin{array}{rcl} H_N(x_1,\ldots,x_N) &=& N\sum_{i=1}^N V(x_i) + \sum_{i\neq j} g(x_i-x_j)\\ &=&N^2\Bigr(\underbrace{\int\!V(x)\mu_N(\mathrm{d} x)+\iint_{x\neq y}g(x-y)\mu_N(\mathrm{d} x)\mu_N(\mathrm{d} y)}_{\mathcal{E}_V^{\neq}(\mu_N)}\Bigr)\\ \end{array} \]
Empirical measure:
\[ \mu_N=\frac{1}{N}\sum_{i=1}^N\delta_{x_i} \]
Boltzmann-Gibbs measure \( {\mathbb{P}_{V,\beta}^N} \) on \( {(\mathbb{R}^d)^N} \):
\[ \frac{\exp\left(-\frac{\beta}{2}H_N(x_1,\ldots,x_N)\right)}{Z_{V,\beta}} = \frac{\exp\left(-\frac{\beta}{2}N^2\mathcal{E}_V^{\neq}(\mu_N)\right)}{Z_{V,\beta}^N} \]
\( {V} \) must be strong enough at infinity to ensure integrability
\( {\mathbb{P}_{N,\beta}} \) is neither product nor log-concave

Empirical measure and equilibrium measure

Random empirical measure under \( {\mathbb{P}_{V,\beta}^N} \):
\[ \mu_N = \frac{1}{N} \sum_{i=1}^N\delta_{x_i}. \]
Under mild assumptions on \( {V} \), with probability one,
\[ \mu_N \underset{N\rightarrow\infty}{\longrightarrow} \mu_V. \]
Large Deviation Principle (Gozlan-C.-Zitt 2014)
\[ \frac{\log\mathbb{P}_{V,\beta}^N\Big(\,\mathrm{dist}(\mu_N,\mu_V) \ge r\Big)}{N^2} \underset{N\rightarrow\infty}{\longrightarrow} -\frac\beta2\inf_{\substack{\mathrm{dist}(\mu,\mu_V)\ge r}} \big(\mathcal{E}_V(\mu)-\mathcal{E}_V(\mu_V)\big). \]
Quantitative estimates? How to relate \( {\mathrm{dist}} \) and \( {\mathcal{E}_V(\cdot)-\mathcal{E}_V(\mu_V)} \)?

Probability metrics and Coulomb transport inequality.

Coulomb divergence (Large Deviations rate function)
\[ \mathcal{E}_V(\mu)-\mathcal{E}_V(\mu_V) \]
Coulomb metric
\[ \sqrt{\mathcal{E}(\mu-\nu)} \]
Bounded-Lipschitz or Fortet–Mourier distance
\[ \mathrm{d}_{{\mathrm{BL}}}(\mu,\nu) =\sup_{\left\|f\right\|_{\mathrm{Lip}}\leq1,\left\|f\right\|_\infty\leq1}\int f(x)(\mu-\nu)(\mathrm{d} x), \]
(Monge-Kantorovich-)Wasserstein distance
\[ \begin{array}{rcl} \mathrm{W}_p(\mu,\nu) &=&\inf_{\substack{(X,Y)\\X\sim\mu,Y\sim\nu}}\mathbb{E}(|X-Y|^p)^{1/p}\\ &=&\Bigr(\inf_{\pi\in\Pi(\mu,\nu)}\iint|x-y|^p\pi(\mathrm{d} x,\mathrm{d} y)\Bigr)^{1/p} \end{array} \]
Kantorovich-Rubinstein duality
\[ \mathrm{W}_1(\mu,\nu)=\sup_{\left\|f\right\|_{\mathrm{Lip}}\leq1}\int\!f(x)(\mu-\nu)(\mathrm{d} x). \]
\[ \mathrm{d}_{{\mathrm{BL}}}(\mu,\nu) \leq\mathrm{W}_1(\mu,\nu) =\sup_{\left\|f\right\|_{\mathrm{Lip}}\leq1}\int\!f(x)(\mu-\nu)(\mathrm{d} x). \]

Local Coulomb transport inequality.

Theorem 1 If \( {D\subset~\mathbb{R}^d} \) compact, \( {\mathrm{supp}(\mu+\nu)\subset D} \), \( {\mathcal{E}(\mu)<\infty} \), \( {\mathcal{E}(\nu)<\infty} \), then
\[ \mathrm{W}_1(\mu,\nu)^2\le C_D\, \mathcal{E}(\mu-\nu). \]

Constant \( {C_D} \) is \( {\approx\mathrm{Vol}(B_{4\mathrm{Vol}(D)})} \)
Extends Popescu local free transport inequality to any dimension \( {d} \)

Idea of proof:

Potential: if \( {U^\mu(x)=g*\mu(x)} \) then \( {\Delta U^\mu(x)=-c_d \,\mu} \)
Electric field: \( {\nabla U^\mu(x)} \). “Carré du champ”: \( {|\nabla U^\mu|^2} \)
Integration by parts and Schwarz’s inequality in \( {\mathbb{R}^d} \) and \( {\mathrm{L}^2} \)
\[ \begin{array}{rcl} c_d\int f(x)(\mu-\nu)(\mathrm{d} x) &=&-\int f(x)\Delta U^{\mu-\nu}(x)\mathrm{d} x\\ &\le&\left\|f\right\|_{\mathrm{Lip}}\Bigr(|D_+| \int|\nabla U^{\mu-\nu}(x)|^2\mathrm{d} x\Bigr)^{1/2} \end{array} \]
Integration by parts again
\[ \begin{array}{rcl} \int|\nabla U^{\mu-\nu}(x)|^2\mathrm{d} x &=&-\int U^{\mu-\nu}(x)\Delta U^{\mu-\nu}(x)\mathrm{d} x \\ &=&c_d\, \mathcal{E}(\mu-\nu). \end{array} \]
Finally \( {\mathrm{W}_1(\mu,\nu)^2\leq|D_+|c_d\mathcal{E}(\mu-\nu)} \).

Coulomb transport inequality for equilibrium measures.

Theorem 2 For any probability measure \( {\mu} \) on \( {\mathbb{R}^d} \) with \( {\mathcal{E}(\mu)<\infty} \)
\[ \mathrm{d}_{{\mathrm{BL}}}(\mu,\mu_V)^2\le C_{{\mathrm{BL}}}\Big(\mathcal{E}_V(\mu)-\mathcal{E}_V(\mu_V)\Big). \]
Moreover if \( {V} \) has at least quadratic growth then
\[ \mathrm{W}_1(\mu,\mu_V)^2\le C_{\mathrm{W}_1}\big(\mathcal{E}_V(\mu)-\mathcal{E}_V(\mu_V)\big). \]

Free transport inequalities (\( {d=2} \) and \( {V=+\infty} \) on \( {\mathbb{R}^c} \))
Extends results by Maïda-Maurel-Segala and Popescu to any dimension \( {d} \)
Growth condition is optimal for \( {\mathrm{W}_1} \)

Concentration of measure for Coulomb gases

Theorem 3 If \( {V} \) does has reasonable growth then for every \( {\beta, N, r} \)
\[ \mathbb{P}_{V,\beta}^N \Big(\mathrm{d}_{{\mathrm{BL}}}(\mu_N,\mu_V)\ge r \Big) \leq \mathrm{e}^{-a\beta N^2 r^2 +\mathbf 1_{d=2}(\frac{\beta}{4} N \log N) +b\beta N^{2-2/d} +c(\beta) N}. \]
Moreover if \( {V} \) has at least quadratic growth then \( {\mathrm{W}_1} \) instead of \( {\mathrm{d}_{{\mathrm{BL}}}} \).

Large deviations principle shows that order in \( {N} \) is optimal
Explicit constants \( {a,b,c} \) if \( {V} \) is quadratic
Implies Wasserstein convergence:
\[ \mathbb{P}_{V,\beta}^N \Big(\mathrm{W}_1(\mu_N,\mu_V)\ge r \Big)\leq \mathrm{e}^{-cN^2r^2}, \quad r\geq \begin{cases} \sqrt{\frac{\log N}{N}}& \mbox{ if } d=2,\\ N^{-1/d} & \mbox{ if } d\geq 3. \end{cases} \]
Recovers, simplifies, and extends certain results by Rougerie and Serfaty

Idea of proof:

Starting point
\[ \mathbb{P}_{V,\beta}^N(\mathrm{W}_1(\mu_N,\mu_V)\geq r) =\frac{1}{Z_{V,\beta}^N}\int_{\mathrm{W}_1(\mu_N,\mu_V)\geq r}\mathrm{e}^{-\frac{\beta}{2}N^2\mathcal{E}_V^{\neq}(\mu_N)}\mathrm{d} x. \]
Normalizing constant
\[ \frac{1}{Z_{V,\beta}^N}\leq \exp\left\{N^2\frac{\beta}{2} \mathcal{E}_V(\mu_V) -N \left(\frac{\beta}{2}\mathcal{E}(\mu_V) -\mathrm{S}(\mu_V)\right)\right\}. \]
Regularization: \( {g} \) superharmonic, \( {\mu_N^{(\varepsilon)}=\mu_N*\lambda_\varepsilon} \),
\[ -N^2\mathcal{E}_V^{\neq}(\mu_N) \leq -N^2\mathcal{E}_V(\mu_N^{(\varepsilon)}) +N\mathcal{E}(\lambda_\varepsilon) +N\sum_{i=1}^N (V*\lambda_\varepsilon -V)(x_i). \]
Coulomb transport \( {-\mathcal{E}_V(\mu_N^{(\varepsilon)})+\mathcal{E}_V(\mu_V)\leq -\frac{1}{C}\mathrm{W}_1^2(\mu_N^{(\varepsilon)},\mu_V)} \).

Concentration for spectrum of Ginibre matrices

Corollary 4 If \( {M} \) is \( {N\times N} \) with iid Gaussian entries of variance \( {\frac{1}{N}} \) in \( {\mathbb{C}} \) then
\[ \mathbb{P}\Big(\mathrm{W}_1(\mu_N,\mu_\bullet)\ge r \Big) \le \mathrm{e}^{ – \frac{1}{4C} N^2 r^2 +\frac{1}{2} N\log N \mathbf + N [\frac{1}{C} +\frac32 -\log\pi]}. \]

Eigenvalues of \( {M} \) has distribution proportional to
\[ \exp(-N\sum_{i=1}^N|x_i|^2)\prod_{i<j}|x_i-x_j|^2 = \exp(-N\sum_{i=1}^N|x_i|^2-\sum_{i\neq j}g(x_i-x_j)) \]
Here \( {d=2} \), \( {\beta=2} \), \( {V=\left|\cdot\right|^2} \)
Provides \( {\lim_{N\rightarrow\infty}\mathrm{W}_1(\mu_N,\mu_\bullet)=0} \) a.s.
Open problem: prove the same for Bernoulli \( {\pm 1} \) random matrices (universality)

Exponential tightness

Theorem 5 For any \( {r\ge r_0} \)
\[ \mathbb{P}_{V,\beta}^N(\mathrm{supp}(\mu_N)\not\subset B_r) = \mathbb{P}_{V,\beta}^N\bigr(\max_{1\le i\le N}|x_i|\ge r\bigr) \le\mathrm{e}^{-cNV_*(r)}, \]
where \( {V_*(r)=\min_{|x|\geq r}V(x)} \).

Follows by using an argument by Borot and Guionnet
Gives that almost surely \( {\varlimsup_{N\rightarrow\infty}\max_{1\le i\le N}|x_i|<\infty} \).
Gives \( {\mathrm{W}_p} \) versions of convergence and concentration
\[ \mathrm{W}_p^p(\mu,\nu) \leq (2M)^{p-1}\mathrm{W}_1(\mu,\nu) \leq M(2M)^{p-1}\mathrm{d}_{\mathrm{BL}}(\mu,\nu). \]
For \( {p=2} \) we get \( {\mathbb{P}_{V,\beta}^N(\mathrm{W}_2(\mu_N,\mu_V)\ge r) \leq 2\mathrm{e}^{-cN^{3/2}r^2}} \).

Convergence in Wasserstein distance for arbitrary temperatures

Corollary 6 If \( {V} \) superquadratic and \( {\beta_N\geq \beta_V\frac{\log N}N} \) then under \( {\mathbb{P}_{V,\beta_N}^N} \) a.s.
\[ \lim_{N\rightarrow\infty}\mathrm{W}_1(\mu_N,\mu_V)=0. \]

Convergence at mesoscopic scale

Corollary 7 We have\ldots
if \( {d=2} \) then
\[ \mathbb{P}_{V,\beta}^N \Big(\mathrm{d}_{{\mathrm{BL}}}\big({\tau^{N^s}_{x_0}}\mu_N,{\tau^{N^s}_{x_0}}\mu_V\big) \geq CN^s\sqrt{\frac{\log N}{N}}\Big)\leq \mathrm{e}^{-cN\log N}, \]
if \( {d\geq 3} \) then
\[ \mathbb{P}_{V,\beta}^N \Big(\mathrm{d}_{\mathrm{BL}}\big({\tau^{N^s}_{x_0}}\mu_N,{\tau^{N^s}_{x_0}}\mu_V\big) \geq CN^{s-1/d}\Big)\leq \mathrm{e}^{-cN^{2-2/d}}. \]
If \( {V} \) superquadratic then \( {\mathrm{d}_{{\mathrm{BL}}}} \) can be replaced by \( {\mathrm{W}_1.} \)
Note that here test functions are global, not local.

Notes and comments

\( {\mathrm{W}_{p\geq 2}} \) versions? Popescu free transport inequalities
Varying \( {V} \) and conditional gases. \( {\mathbb{P}_{V,\beta}^N(\cdot\mid x_N)=\mathbb{P}_{\widetilde V_N,\beta}^{N-1}} \) with
\[ \widetilde V_N=\frac{N}{N-1}V+\frac{2}{N-1}g(x_N-\cdot) \]
[covered by our work since \( {g} \) is superharmonic]
Usage for CLT with GFF in all dimensions
Weakly confining potentials and heavy-tailed \( {\mu_V} \)
Universality of concentration for random matrices
Crossover and Sanov regime \( {\beta_N\propto N} \)
Concentration around the mean \( {\mathbb{P}^N_{V,\beta}(\mathrm{d}(\mu_N,\mathbb{E}\mu_N)\geq r)} \) and bias \( {\mathrm{d}(\mathbb{E}\mu_N,\mu_V)} \)
Dynamical aspects (in progress, see arXiv:1706.08776)

Further reading (randomly sampled)

Some other posts: