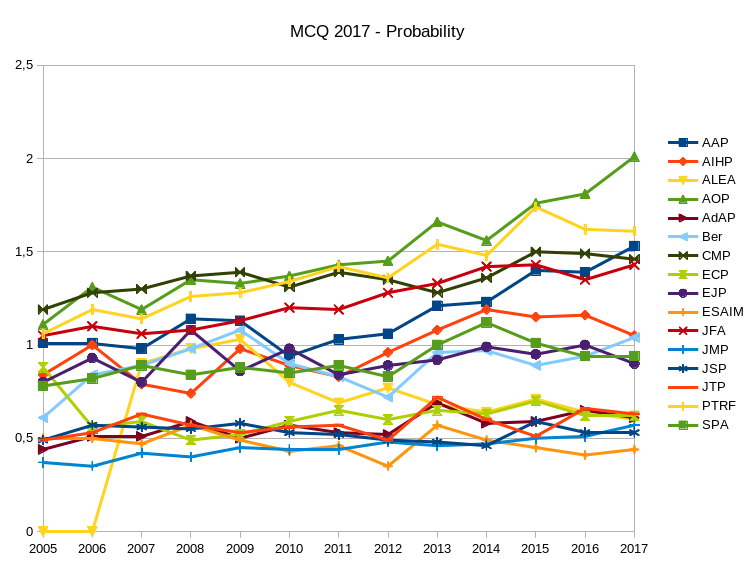
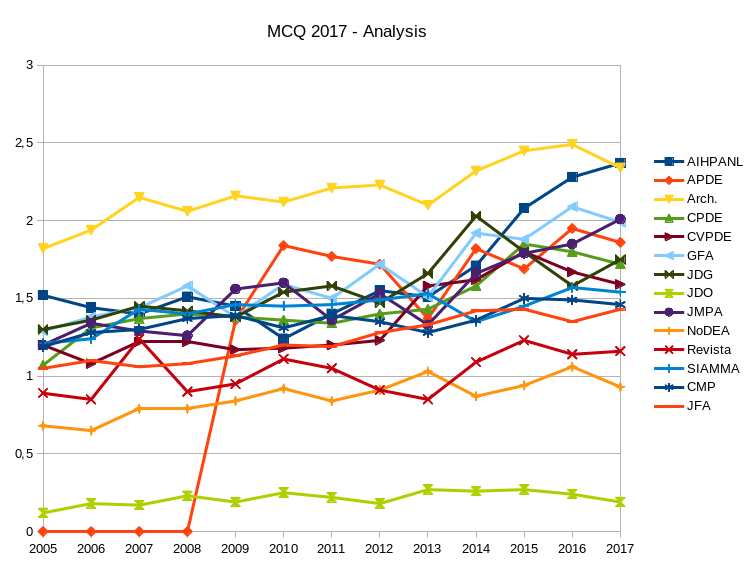
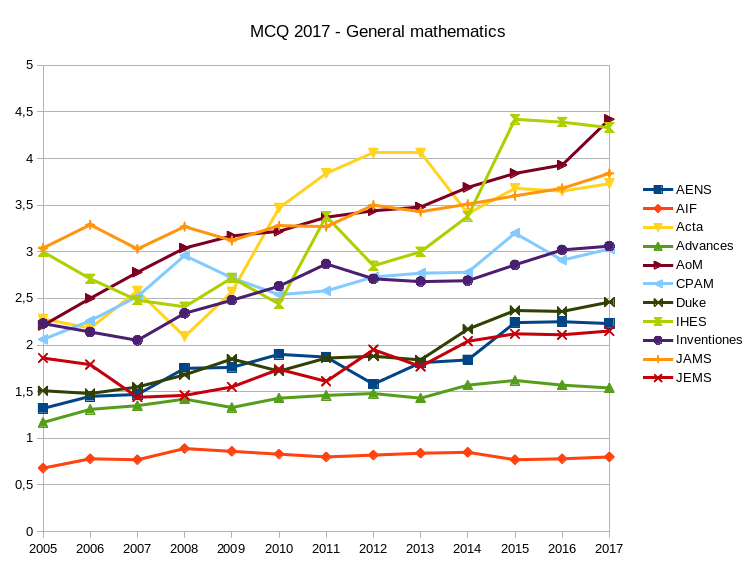
Here are the Mathematical Citation Quotient (MCQ) for journals in probability, statistics, analysis, and general mathematics. The numbers were obtained using a home brewed Python script extracting data from MathSciNet. The graphics were obtained by using LibreOffice.
Recall that the MCQ is a ratio of two counts for a selected journal and a selected year. The MCQ for year $Y$ and journal $J$ is given by the formula $\mathrm{MCQ}=m/n$ where
- $m$ is the total number of citations of papers published in jounal $J$ in years $Y-1$,...,$Y-5$ by papers published in year $Y$ in any journal known by MathSciNet;
- $n$ is the total number of papers published in journal $J$ in years $Y-1$,...,$Y-5$.
The Mathematical Reviews compute every year the MCQ for every indexed journal, and make it available on MathSciNet. This formula is very similar to the one of the five years impact factor, the main difference being the population of journals which is specifically mathematical for the MCQ (reference list journals) and the way the citations are extracted. Both biases are negative.
1 Comment