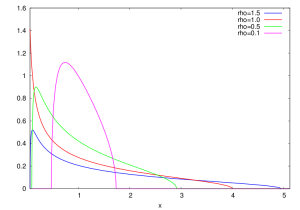
The Marchenko-Pastur law

The Marchenko – Pastur law \( {\mu_\rho} \) with shape parameter \( {\rho>0} \) is the probability distribution

\[ \left(1-\frac{1}{\rho}\right)_+\delta_0+\frac{1}{\rho 2\pi x}\sqrt{(b-x)(x-a)}\,\mathbf{1}_{[a,b]}(x)dx \]

where

\[ a=(1-\sqrt{\rho})^2 \quad\text{and}\quad b=(1+\sqrt{\rho})^2. \]

It has mean \( {1} \) and variance \( {\rho} \). It has an atom at point \( {0} \) if and only if \( {\rho>1} \).

Lemma 1 (Moments of the Marchenko-Pastur law) For all \( {r\geq1} \),

\[ \int\!x^r\,d\mu_\rho(x) =\sum_{k=0}^{r-1}\frac{\rho^k}{k+1}\binom{r}{k}\binom{r-1}{k}. \]

Proof: Since \( {a+b=2(1+\rho)} \) and \( {ab=(1-\rho)^2} \) we have

\[ \sqrt{(b-x)(x-a)} =\sqrt{\frac{(a+b)^2}{4}-ab-\left(x-\frac{a+b}{2}\right)^2} =\sqrt{4\rho-(x-(1+\rho))^2} \]

The change of variable \( {y=(x-(1+\rho))/\sqrt{\rho}} \) gives

\[ \int\!x^r\,d\mu_\rho(x) =\int\!x^r\,d\mu_\rho(x) =\frac{1}{2\pi} \int_{-2}^2\!(\sqrt{\rho}y+1+\rho)^{r-1}\sqrt{4-y^2}\,dy. \]

Recall that the moments of the semicircle law are given by the Catalan numbers :

\[ \frac{1}{2\pi}\int_{-2}^2\!y^{2k+1}\,\sqrt{4-y^2}\,dy =0 \quad\text{and}\quad \frac{1}{2\pi}\int_{-2}^2\!y^{2k}\,\sqrt{4-y^2}\,dy =\frac{1}{1+k}\binom{2k}{k}. \]

This gives, by using binomial expansions and Vandermonde’s identity

\[ \begin{array}{rcl} \int\!x^r\,d\mu_\rho(x) &=&\sum_{k=0}^{\lfloor(r-1)/2\rfloor} \rho^k(1+\rho)^{r-1-2k}\binom{r-1}{2k}\binom{2k}{k}\frac{1}{1+k}\\ &=&\sum_{k=0}^{\lfloor(r-1)/2\rfloor} \rho^k(1+\rho)^{r-1-2k}\frac{(r-1)!}{(r-1-2k)!k!(k+1)!}\\ &=&\sum_{k=0}^{\lfloor(r-1)/2\rfloor} \sum_{s=0}^{r-1-2k} \rho^{k+s}\frac{(r-1)!}{k!(k+1)!(r-1-2k-s)!s!}\\ &=&\sum_{t=0}^{r-1}\rho^t\sum_{k=0}^{\min(t,r-1-t)} \frac{(r-1)!}{k!(k+1)!(r-1-t-k)!(t-k)!}\\ &=&\frac{1}{r}\sum_{t=0}^{r-1}\rho^t\binom{r}{t}\sum_{k=0}^{\min(t,r-1-t)} \binom{t}{k}\binom{r-t}{k+1}\\ &=&\frac{1}{r}\sum_{t=0}^{r-1}\rho^t\binom{r}{t}\binom{r}{t+1} \\ &=&\sum_{t=0}^{r-1}\frac{\rho^t}{t+1}\binom{r}{t}\binom{r-1}{t}. \end{array} \]

☐ The Marchenko-Pastur law appears in the famous Marchenko-Pastur theorem. Namely, let \( {X_1,\ldots,X_n} \) be independent and identically distributed random column vectors of \( {\mathbb{R}^m} \), with mean \( {0} \) and covariance matrix \( {I_m} \). Let us consider the \( {m\times m} \) empirical covariance matrix

\[ \frac{1}{n}\sum_{i=1}^nX_iX_i^\top=\frac{1}{n}YY^\top \quad\text{where}\quad Y=\left(X_1\cdots X_n\right). \]

We have \( {\mathbb{E}(\frac{1}{n}YY^\top)=I_m} \) and the strong law of large numbers indicates that with probability one,

\[ \lim_{n\rightarrow\infty}\frac{1}{n}YY^\top = I_m. \]

What happens if \( {m} \) grows with \( {n} \)? Let us assume for simplicity that the components of \( {X_1} \) are independent (automatic if \( {X_1} \) is Gaussian).

Theorem 2 (Marchenko-Pastur) Suppose that \( {m=m_n} \) depends on \( {n} \) is such a way that

\[ \lim_{n\rightarrow\infty}\frac{m_n}{n}=\rho\in(0,\infty). \]

Let \( {\lambda_{n,1},\ldots,\lambda_{n,m_n}\in[0,\infty)} \) be the eigenvalues of the \( {m_n\times m_n} \) empirical covariance matrix \( {\frac{1}{n}YY^\top} \), and let us consider the empirical spectral distribution

\[ \mu_n:=\frac{1}{m_n}\sum_{k=1}^{m_n}\delta_{\lambda_{n,k}}. \]

Then with probability one, for every bounded continuous \( {f:\mathbb{R}\rightarrow\mathbb{R}} \),

\[ \lim_{n\rightarrow\infty}\int\!f\,d\mu_n=\int\!f\,d\mu_\rho \]

In other words, with probability one, for every \( {x\in\mathbb{R}} \) (\( {x\neq0} \) if \( {\rho>1} \)), denoting \( {I=(-\infty,x]} \),

\[ \lim_{n\rightarrow\infty}\mu_n(I)=\mu_\rho(I). \]

Note that

\[ \int\!x\,d\mu_n=\frac{1}{m_n}\sum_{k=1}^{m_n}\lambda_{n,k} =\frac{1}{m_n}\mathrm{Tr}\left(\frac{1}{n}YY^\top\right) =\frac{1}{nm_n}\sum_{\substack{1\leq i\leq m_n\\1\leq j\leq n}}Y_{ij}^2 \]

and thus, by the strong law of large numbers, with probability one,

\[ \lim_{n\rightarrow\infty} \int\!x\,d\mu_n = 1 =\int\!x\,d\mu_\rho(x). \]

This shows the almost sure convergence of the first moment. It shows also that the sequence \( {{(\mu_n)}_{n\geq1}} \) is tight with probability one since by Markov’s inequality, for all \( {r>0} \),

\[ \mu_n([0,r]^c) \leq \frac{1}{r}\int\!x\,d\mu_n. \]

The Marchenko-Pastur theorem can be proved by using the method of moments or the Cauchy-Stieltjes resolvent method. In the Gaussian case, one may also use orthogonal polynomials (in this case the empirical covariance matrix belongs to the Laguerre Ensemble and its law is Wishart). Useful references include the recent book by Bai and Silverstein and the forthcoming book of Pastur and Shcherbina. Regarding orthogonal polynomials, there is a differential operator approach due to Haagerup and Thorbjørnsen, developped by Ledoux, in which the Marchenko-Pastur distribution is recovered as a mixture of a uniform and arcsine distributions. In free probability theory, the Marchenko-Pastur law is known as the free Poisson law, see for instance the book by Nica and Speicher or the book by Hiai and Petz.

If \( {\rho=1} \) then \( {\frac{1}{n}YY^\top} \) is asymptotically square, \( {a=0} \), \( {b=4} \), and the change of variable \( {t\mapsto\sqrt{t}} \) shows that with probability one, the empirical spectral distribution of

\[ \sqrt{\frac{1}{n}YY^\top} \]

converges as \( {n\rightarrow\infty} \) to the quarter circle law with density

\[ \frac{1}{\pi}\sqrt{4-x^2}\,\mathbf{1}_{[0,2]}(x)dx. \]

Concerning the support of the spectrum, one may first order the spectrum of \( {\frac{1}{n}YY^\top} \) as follows:

\[ \lambda_{n,1}\geq\cdots\geq\lambda_{n,m}. \]

Note that \( {\lambda_{n,k}=0} \) if \( {k>\min(m,n)} \). We have then the following:

Theorem 3 (Bai-Yin) Under the assumptions of the Marchenko-Pastur theoren and if additionnaly \( {X_{11}} \) have a finite fourth moment then with probability one

\[ \lim_{n\rightarrow\infty}\lambda_{n,\min(m,n)}=b \quad\text{and}\quad \lim_{n\rightarrow\infty}\lambda_{n,1}=a. \]

The Marchenko-Pastur theorem remains valid even if \( {X_{11}} \) does not have a zero mean, in contrast with the Bai-Yin theorem which fails in that case. The edge of the spectrum of \( {\frac{1}{n}YY^\top} \) is sensitive to finite rank perturbations of \( {Y} \) while the bulk of the spectrum is not, asymptotically.

Dimensional noise. The Marchenko-Pastur law has mean \( {1} \) and variance \( {\rho} \). It is enlightening to set \( {1_\pm=(1\pm\sqrt{\rho})^2} \), making apparent that the support \( {[a,b]=[1_-,1_+]} \) of the Marchenko-Pastur law is an interval around the mean \( {1} \), which is the spectrum of the population covariance matrix \( {I_m} \). This noise is a high dimensional effect due to the fact that \( {m} \) as well as \( {n} \) go to infinity.

Quarter circular law. If \( {\rho=1} \) then \( {[1_-,1_+]=[0,4]} \) and the Marchenko-Pastur law becomes

\[ \frac{\sqrt{4-x}}{2\pi\sqrt{x}}\mathbf{1}_{x\in[0,4]}\mathrm{d}x, \]

and its image by the map \( {x\mapsto\sqrt{x}} \) in this case is then the quartercircle law

\[ \frac{\sqrt{4-x^2}}{\pi}\mathbf{1}_{x\in[0,2]}\mathrm{d}x. \]

Shape parameter. The image of the Marchenko-Pastur law by the map \( {x\mapsto\frac{x-(1+\rho)}{\sqrt{\rho}}} \) is

\[ \frac{\sqrt{4-x^2}}{2\pi(1+\rho+\sqrt{\rho}x)}\mathbf{1}_{x\in[-2,2]}\mathrm{d}x, \]

which reveals that \( {\rho} \) is a shape rather than a scale parameter around the mean. This makes also apparent the convergence to the Wigner semicircle law as \( {\rho\rightarrow0} \).