Djalil CHAFAÏ (شافعي جليل)
Mathematician - University professor
- Université Paris-Dauphine - PSL • CEREMADE • Place du Maréchal de Lattre de Tassigny, 75775 Paris Cedex 16
- Made available (« mis à disposition ») by Dauphine to École normale, from September 2021 to August 2031
- Email. firstname@lastname.net (without diacritics)
Current duties include...
- Directeur scientifique du RNBM (2021 - 2025) après Frédéric Hélein
Research topics up to now
- Geometric and probabilistic functional analysis, concentration, convexity, isoperimetry
- Random matrices, random graphs, free probability, and high dimensional phenomena
- Convexity and positivity, variational analysis, potential theory
- Asymptotic analysis, exact solvability, special functions
- Stochastic models and stochastic inverse problems:
- Mathematical Biology (pharmacology, biostatistics)
- Mathematical Physics (spin systems, interacting particle systems, statistical physics)
- Data Science (data streams processing, queuing, machine learning, decision making)
- Earth Science (variational assimilation in meteorology)
- Random structures and algorithms, stochastic simulation
- Markov processes/semigroups, their equilibrium/geometry
- Sobolev type inequalities and partial differential equations
- Poisson and Gauss measures, heat kernels, limit theorems
- Boltzmann-Shannon and Voiculescu entropies, information theory, operator theory

Pictures
Some pictures illustrating my research, created mostly with Octave, Python, or Julia. Enjoy visual mathematics!
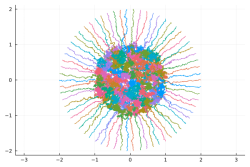
- Left: Spectrum of a high dimensional square matrix with heavy tailed (infinite variance) iid entries:
Right: Voronoi cells of the spectrum of a high dimensional matrix with iid Gaussian entries:


More in arXiv:1006.1713 and in arXiv:1109.3343 - Trajectories of an eight particles Hamilton-Monte-Carlo algorithm for a one-dimensional log-gas:
More in arXiv:1806.05985 - Phase portrait of the reciprocal polynomial of the characteristic polynomial of a high dimensional Gaussian matrix (left: complex, right: real):


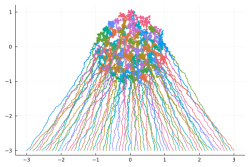
More in arXiv:2012.05602 and Blogpost - Left: three independent real Brownian motion (time in horizontal axis):
Center: the same BMs with a quadratic confinement making them three independent Ornstein-Uhlenbeck (OU) processes:
Right: the same OUs with singular repulsion making them a single three particles Dyson-Ornstein-Uhlenbeck process:
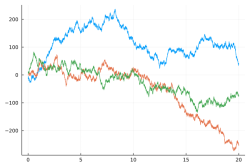
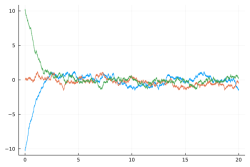
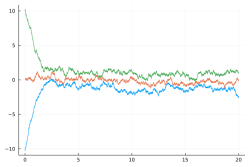
More in arXiv:2107.14452 Talk slides - Trajectory of a planar Dyson Ornstein-Uhlenbeck process with 66 particles started from a uniform grid on circle or line:
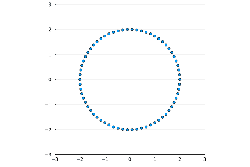

Click on picture to see animation. More in arXiv:1706.08776 and in Blogpost - Equilibrium measures of planar Coulomb gas with various conditionings on linear statistics:

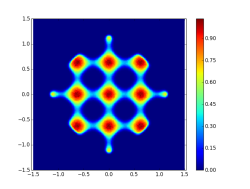


These pictures are courtesy of my co-author Grégoire Ferré. More in arXiv:1907.05803 - Equilibrium measure in dimension 4 for log‖⋅‖2 repulsion and ‖⋅‖44 confinement, projected on first three coordinates:
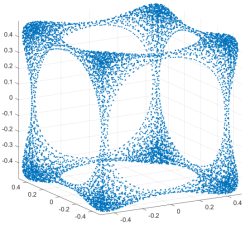
This picture is courtesy of my co-author Robert S. Womersley. More in arXiv:2206.04956
Doctoral and postdoctoral advisory
- Current doctoral students
- Samuel Chan-ashing (2024-, Paris-Dauphine - PSL, with Quentin Cormier)
Long time behavior of diffusion processes : cutoff phenomenon and metastability - Rémi Bonnin (2024-, Aix-Marseille Université, with Charles Bordenave)
High dimensional random tensors - Kewei Pan (2023-, Toulouse, with Guillaume Cébron)
Around Boolean entropy, random matrices, and Coulomb gases - Quentin François (2022-, Paris-Dauphine - PSL, with Pierre Tarrago)
Random Matrices : high dimension and exact solvability
- Former postdoctoral researchers
- Guillaume Dubach (2022-2023, FSMP)
Probability theory, especially random matrices
Actuellement professeur Monge à l'École polytechnique
-
- Hugo Magaldi (Paris-Dauphine - PSL 2022, with Laure Dumaz)
Étude des beta-ensembles et leur limite à haute température
Actuellement ingénieur - Jeanne Boursier (Paris-Dauphine - PSL 2022, with Sylvia Serfaty)
Quelques problèmes de mécanique statistique pour les gaz de Coulomb et de Riesz
Postdoctoral fellow, J.F. Ritt Assistant Professor, Columbia University, New York - Josué Corujo (Paris-Dauphine - PSL 2021, with Simona Grusea)
Multi-allelic Moran models and quasi-stationary distributions
Actuellement maître de conférences à l'Université Paris-Est Créteil - Ezéchiel Kahn (École des Ponts ParisTech 2021, with Benjamin Jourdain)
Matrices de covariance : diffusions, probabilités libres, et apprentissage profond
Actuellement haut fonctionnaire du Corps des Ponts, des Eaux, et des Forêts - David García-Zelada (Paris-Dauphine - PSL 2019)
Aspects géométriques et probabilistes des gaz de Coulomb
Actuellement maître de conférences à Sorbonne Université - Raphaël Butez (Paris-Dauphine - PSL 2017)
Polynômes aléatoires, gaz de Coulomb, et matrices aléatoires
Actuellement maître de conférences à l'université de Lille - Marie-Noémie Thai (Marne-la-Vallée / Paris-Est 2015, with Amine Asselah)
Processus de Fleming-Viot, distributions quasi-stationnaires et marches aléatoires en interaction de type champ moyen
Actuellement enseignante à l'École supérieure d'ingénieurs Léonard-de-Vinci - Bertrand Cloez (Marne-la-Vallée / Paris-Est 2013)
Comportement asymptotique de processus avec sauts et applications pour des modèles avec branchement
Actuellement chargé de recherches à l'INRAE - Julie Champion (Toulouse 2013, with Franck Barthe)
Sur les algorithmes de projection en entropie relative avec contraintes marginales
Actuellement professeure en classes préparatoires aux grandes écoles - Julie Antic (Toulouse 2009, with Didier Concordet)
Nonparametric methods for population PK and/or PD
Actuellement ingénieure dans l'industrie spatiale
Animation
Voici quelques activités d'animation dans le cadre du milieu professionnel mais en dehors de l'enseignement et de la recherche canoniques.
- Après-midi des lycéens à l'ÉNS 2024 (participation en tant qu'orateur)
- Après-midi des lycéens à l'ÉNS 2025 (conception et organisation)
- Journées ÉNS - CPGE 2025 - Autour du prix Abel de Michel Talagrand (conception et organisation)
- Journées ÉNS - CPGE 2024 - Géométries (conception et organisation)
- Journées ÉNS - CPGE 2023 - Autour des médailles Fields 2022 (conception et organisation)
- PSL Week 2023 : Modéliser le monde réel, pratiques et limites (conception et organisation)
- Week-end DMA 2024 - Le Tréport et Amiens (conception et organisation)
- Week-end DMA 2023 - Étretat et Jumièges (conception et organisation)
Agenda
Scientific life in Dauphine and École normale
Conferences, schools, days, ...
Projects membership (only running projects)
Papers
You may read Publications: science, money, and human comedy on my blog.
Digital footprint in professional data bases :
Partial list of publications automatically provided by arXiv :
Djalil Chafai's articles on arXiv
- [1] http://arxiv.org/abs/2412.15969v2 [ html pdf ]
- [2] http://arxiv.org/abs/2503.11770v1 [ html pdf ]
- [3] http://arxiv.org/abs/2405.00120v1 [ html pdf ]
- [4] http://arxiv.org/abs/2212.06090v2 [ html pdf ]
- [5] http://arxiv.org/abs/2206.04956v3 [ html pdf ]
- [6] http://arxiv.org/abs/2108.00534v6 [ html pdf ]
- [7] http://arxiv.org/abs/2107.14452v3 [ html pdf ]
- [8] http://arxiv.org/abs/2108.10653v2 [ html pdf ]
- [9] http://arxiv.org/abs/2012.05602v2 [ html pdf ]
- [10] http://arxiv.org/abs/2012.04633v2 [ html pdf ]
- [11] http://arxiv.org/abs/1907.05803v3 [ html pdf ]
- [12] http://arxiv.org/abs/1607.02741v3 [ html pdf ]
- [13] http://arxiv.org/abs/1909.00613v2 [ html pdf ]
- [14] http://arxiv.org/abs/1805.00708v3 [ html pdf ]
- [15] http://arxiv.org/abs/1806.05985v4 [ html pdf ]
- [16] http://arxiv.org/abs/1607.05484v2 [ html pdf ]
- [17] http://arxiv.org/abs/1706.08776v3 [ html pdf ]
- [18] http://arxiv.org/abs/1610.00980v3 [ html pdf ]
- [19] http://arxiv.org/abs/1610.01836v2 [ html pdf ]
- [20] http://arxiv.org/abs/1509.02231v1 [ html pdf ]
- [21] http://arxiv.org/abs/1405.1003v4 [ html pdf ]
- [22] http://arxiv.org/abs/1304.7569v4 [ html pdf ]
- [23] http://arxiv.org/abs/1310.0727v2 [ html pdf ]
- [24] http://arxiv.org/abs/1202.0644v3 [ html pdf ]
- [25] http://arxiv.org/abs/1402.3660v1 [ html pdf ]
- [26] http://arxiv.org/abs/1011.2331v4 [ html pdf ]
- [27] http://arxiv.org/abs/1303.5838v1 [ html pdf ]
- [28] http://arxiv.org/abs/0903.3528v5 [ html pdf ]
- [29] http://arxiv.org/abs/1109.3343v4 [ html pdf ]
- [30] http://arxiv.org/abs/1006.1713v5 [ html pdf ]
- [31] http://arxiv.org/abs/1104.2198v1 [ html pdf ]
- [32] http://arxiv.org/abs/0808.1502v3 [ html pdf ]
- [33] http://arxiv.org/abs/0811.1097v2 [ html pdf ]
- [34] http://arxiv.org/abs/0709.0036v3 [ html pdf ]
- [35] http://arxiv.org/abs/0805.0987v3 [ html pdf ]
- [36] http://arxiv.org/abs/0811.2180v3 [ html pdf ]
- [37] http://arxiv.org/abs/0709.4678v3 [ html pdf ]
- [38] http://arxiv.org/abs/0811.0600v2 [ html pdf ]
- [39] http://arxiv.org/abs/0805.1971v2 [ html pdf ]
- [40] http://arxiv.org/abs/0709.0111v2 [ html pdf ]
- [41] http://arxiv.org/abs/0710.3139v5 [ html pdf ]
- [42] http://arxiv.org/abs/math/0412193v3 [ html pdf ]
- [43] http://arxiv.org/abs/math/0507102v2 [ html pdf ]
- [44] http://arxiv.org/abs/math/0510488v2 [ html pdf ]
- [45] http://arxiv.org/abs/math/0411516v1 [ html pdf ]
- [46] http://arxiv.org/abs/math/0211108v1 [ html pdf ]
- [47] http://arxiv.org/abs/math/0211103v2 [ html pdf ]
- [48] http://arxiv.org/abs/math/0102227v1 [ html pdf ]
[ Showing 48 of 48 total entries]
Books
Authored books
Edited books
Authored pedagogical books
Documents
Talk slides and videos
Classes préparatoires aux grandes écoles
Unpublished reports and expository notes
Selected texts and tribunes
Teaching
Ce que l'on conçoit bien s'énonce clairement et les mots pour le dire arrivent aisément.
Nicolas Boileau, L'art poétique (1674) Chant I.
J'ajouterais quant à moi que la réciproque n'est pas forcément juste. Méfiez vous des beaux parleurs !
ÉNS (Master 1 S1) : Processus stochastiques
ÉNS (Licence 3 S1) : Topologie et calcul différentiel
ÉNS (Licence 3 S2) : Phénomènes de grande dimension
ÉNS (Master 2 S2) : High-Dimensional Probability
PSL - Master 2 : A review of probability theory foundations (pre-school)
PSL - Master 2 : Introduction to Stochastic Calculus
Dauphine-PSL - Master 2 : Logarithmic Sobolev Inequalities Essentials
École Polytechnique - Probabilités (2011-2017)
Dauphine-PSL - Master 1 : Introduction aux séries temporelles
Marne-la-Vallée & Dauphine-PSL - Master 2 : Stochastic Models
Toulouse & Rennes & Marne-la-Vallée - Cours Master 2 : Modèles markoviens en biologie
Biskra & Oran - Master 1 : Chaînes de Markov
Marne-la-Vallée - Préparation à l'agrégation interne : probabilités et statistique
Toulouse - Préparation à l'agrégation externe : oral de modélisation option probabilités et statistique (option A)
Quelques liens
Software (C++, LaTeX, Python, C#, Julia, ...)

- Simcoul Julia code
In collaboration with Grégoire Ferré
Julia code for simulation of Coulomb gases and more with HMC
Git repository on CNRS/PLM GitLab - The w2m.py Python module/script
Python web spider walking through a subset of WWW and producing an adjacency matrix
Module on PyPi Git repository on GitHub - The ejpecp LaTeX2ε class
In collaboration with Krzysztof Burdzy
LaTeX2ε document class for Electronic Journal of Probability and Electronic Communications in Probability
LaTeX Package on CTAN - Computational Rough Paths (CoRoPa)
In collaboration with Terry J. Lyons
C++ template classes libraries handling tree structures and free Lie algebras, including Campbell-Baker-Hausdorff formula, shuffle product, Dynkin map, dynamic Hall bases, etc. Based on STL and compatible with GMP
Webpage and package on SourceForge - The Girko circular law in Python via SageMathCell
xxxxxxxxxximport numpy as npimport matplotlib.pyplot as ppn = 66; r = 66; for i in range(1,r+1): M = np.sign(np.random.randn(n,n))/np.sqrt(n); # Real Bernoulli # M = np.random.randn(n,n)/np.sqrt(n); # Real Ginibre # M = (np.random.randn(n,n)+1j*np.random.randn(n,n))/np.sqrt(2*n); # Complex Ginibre S = np.linalg.eigvals(M); pp.plot(S.real,S.imag,'k.')pp.axis("equal")pp.title("Circular law")pp.legend()pp.show()Miscellany
You said Miscellany?
- Read and write my name
- On my passports and ID cards, my name is written Djalil Chafaï
- Read Djalil like you read it in Django Reinhardt (thanks Jack!)
- Djalil is my first name and Chafaï is my surname or lastname or family name
- English speaking people should read my name as Jalil Shaf-i-e
- French speaking people should read it as Djè-lil Chaf-aille-i
- Arabic speaking people may read it directly شاﻓﻌﻲ جلیل
- All the rest of the world may read IPA ʃaːfɪʕɪ dʒəlɪl
- For (La)TeX you may write
Djalil Chafa\“{\i} - For ArabTeX you may use
^sAfi`iy ^galiyl - For HTML just write
Djalil Chafaï
- Numbers
- Favourite prime number is 15061973, the 974461th
- Molecules
- I also taste CH3CH2OH in good wines such as Château Peyrines (F-33410 Cadillac, France)
- Paul Sabatier Reaction: CO2 + 4H2 → CH4 + 2H2O
- Popular science?
- À vrai dire, je n'aime pas beaucoup le terme « vulgarisation » qui a la même racine que le mot péjoratif « vulgaire ». Il faudrait forger un nouveau terme qui signifierait « rendre accessible avec enthousiasme en excitant la curiosité ».
- Social mathematics
- Mathematical collections
- Blogs
- Papers
- Computer Science
- {0,1}∞ on my blog
- Have you heard about the Gödel prize? and the Turing award?
- Probability
- Provocation: « Si tu ne sais pas ce que c'est que les probabilités, c'est probablement ce qui te manque pour comprendre la physique ! »
- « Un homme tirait au sort toutes ses décisions. Il ne lui arriva pas plus de mal qu'aux autres qui réfléchissent. »
Paul Valéry, Choses Tues, Oeuvres II, Pléiade, p. 505.
Denis Talay : « Et s'il avait réfléchi en plus de tirer au sort ? »
- Numerical Analysis
- Volker Strassen, from the law of the iterated logarithm to matrix multiplications
- Mathematics & Biology
- Mathematics & Physics
- «Le physicien traite les problèmes du véhicule à une roue (la brouette), à deux roues (tilbury ou bicyclette), à trois, à quatre roues. Le mathématicien traite le problème général du véhicule à n roues, n étant entier ou fractionnaire, positif ou négatif, réel ou imaginaire.»
Henri Bouasse
- Free software
- « Don't forget that Linux became only possible because 20 years of OS research was carefully studied, analyzed, discussed and thrown away. »
Ingo Molnár - « This is the Unix philosophy: Write programs that do one thing and do it well. Write programs to work together. Write programs to handle text streams, because that is a universal interface. »
Doug McIlroy
- Minds
- Beyond pure science: Jean Bricmont and Noam Chomsky
- Englishman: Harold Pinter
- Middle East: Avraham Burg and Shlomo Sand
- Europe
- Literature (or « lis tes ratures »)
- Michel Houellebecq (1958 - )
- « Alice posait sur nous ce regard à la fois affectueux et légèrement moqueur des femmes qui suivent une conversation entre hommes, cette chose curieuse qui semble toujours hésiter entre la pédérastie et le duel. »
in Soumission p. 58 (2015) - « Il avait un cachet “intellectuel de droite” assez séduisant, me dis-je, ça lui assurait une petite singularité à la fac. On peut laisser parler les gens assez longtemps, ils sont toujours intéressés par leur propre discours, mais il faut quand même relancer de temps en temps, un minimum. »
in Soumission p. 60 (2015)
- Alexandre Soljenitsyne (1918 - 2008)
- « Peu à peu, j’ai découvert que la ligne de partage entre le bien et le mal ne sépare ni les États ni les classes ni les partis, mais qu’elle traverse le cœur de chaque homme et de toute l’humanité. »
- Art
- Pablo Picasso (1881 - 1973)
- « La inspiración existe, pero tiene que encontrarte trabajando » (”Inspiration exists, but it has to find you working)“
in Tomás R. Villasante (1994), Las ciudades hablan: identidades y movimientos sociales en seis metrópolis latinoamericanas. p. 264.
- Guy Ribes (1948 - )
- « Comme pour n'importe quel tableau, chaque faux suppose une recherche. Un peintre, qu'il soit faussaire ou non, est, toute sa vie, un étudiant qui se met à l'école de l'art. Je n'ai pas fait un seul Matisse ou un seul Renoir, je les ai faits en dix exemplaires, jusqu'à ce que je comprenne leur nature et leur sens. On ne peut pas créer une œuvre de cette importance du premier coup. On commet des erreurs, on détruit, on recommence… »
in Autoportrait d'un faussaire p. 120 (2015)
- Mathematicians and physicists
- Free probability: Eugene P. Wigner and John von Neumann were schoolmates in Budapest and colleagues in Princeton. Their works were connected by Dan-Virgil Voiculescu, a romanian-american mathematician.
- Didier Concordet (1962 - )
- «D'année en année, les étudiants sont de plus en plus jeunes. »
- Roger-Dominique Bakry (1954 - × )
- « Y'a qu'un nombre fini d'idées. »
- « À part Cauchy-Schwarz… » and more recently « À part Pythagore… »
- « Ce qui compte, en maths, c'est les idées »
- « En général, dans un papier, entre l'abstract et le non-sense, il y a l'introduction »
- « De toute manière, tous les papiers sont faux, et ça n'est pas grave, car personne ne les lit »
- « Tu ferais mieux de te trouver un vrai métier… »
- James Clerk Maxwell (1831 - 1879)
- «… They say that Understanding ought to work by the rules of right reason. These rules are, or ought to be, contained in Logic; but the actual science of Logic is conversant at present only with things either certain, impossible, or entirely doubtful, none of which (fortunately) we have to reason on. Therefore the true Logic for this world is the Calculus of Probabilities, which takes account of the magnitude of the probability (which is, or which ought to be in a reasonable man's mind). This branch of Math., which is generally thought to favour gambling, dicing, and wagering, and therefore highly immoral, is the only “Mathematics for Practical Men,” as we ought to be. … James Clerk Maxwell (1850) Letter to Lewis Campbell; reproduced in L. Campbell and W. Garrett, The Life of James Clerk Maxwell, Macmillan, 1881, page 80.
- Mark Kac (1914 - 1984)
- «I prefer concrete things and I don't like to learn more about abstract stuff than I absolutely have to. »
- Henri Poincaré (1854 - 1912)
- À propos de la loi normale du théorème central limite, désigné sous le nom de loi des erreurs à l'époque : « Cette loi ne s'obtient pas par des déductions rigoureuses ; plus d’une démonstration qu’on a voulu en donner est grossière, entre autres celle qui s’appuie sur l’affirmation que la probabilité des écarts est proportionnelle aux écarts. Tout le monde y croit cependant, me disait un jour M. Lippmann, car les expérimentateurs s’imaginent que c’est un théorème de mathématiques, et les mathématiciens que c’est un fait expérimental. » In Le calcul des Probabilités (1896) p. 149). Comme le dit le physicien Oriol Bohigas, de nos jours, nous savons que c'est à la fois un fait expérimental et un théorème de mathématiques !
- Bruno de Finetti (1906 - 1985)
- «…Mathematics is not by now a field already explored, just to learn and pass on to posterity as it is. It is always progressing, it is enriching and lightening itself, it is a lively and vital creature, in full development and just for these reasons I love it, I study it and I wish to devote my life to it…»
- Philippe Biane (1962 - )
- Les probabilités et le mouvement brownien (Vidéo, magnifique cravate)
- Vladimir Arnold (1937 - 2010)
- La mathématique expérimentale (Vidéo)
- « Les mathématiques ne sont qu'un chapitre de la physique ! »
- Jean-Pierre Serre (1926 - )
- How to write mathematics badly (Video)
- Bernard Beauzamy (1947 - )
- Les erreurs en mathématiques (Vidéo)
-
- Jean-Philippe Bouchaud (1962 - )
-
- Bernard Derrida (1952 - )
- Physique statistique (Vidéo)
-
- « There are several categories of scientists in the world; those of second or third rank do their best but never get very far. Then there is the first rank, those who make important discoveries, fundamental to scientific progress. But then there are the geniuses, like Galilei and Newton. Majorana was one of these. » 1938, about Ettore Majorana
- Ludwig Boltzmann (1844 - 1906)
- « … If you ask me about my innermost conviction whether our century will be called the century of iron or the century of steam or electricity, I answer without hesitation: It will be called the century of the mechanical view of Nature, the century of Darwin. … »
- John Forbes Nash Jr. (1928 - 2015)
- « The ideas I had about supernatural beings came to me the same way that my mathematical ideas did. So I took them seriously. »
- Gian-Carlo Rota (1932 - 1999)
- Ten Lessons I Wish I Had Been Taught Notices on the AMS 44 (1997)
- « Don't fight with success »
- « You should only listen to advice that you do not have to follow »
- Paul Halmos (1916 - 2006)
- « Don't just read it; fight it! Ask your own questions, look for your own examples, discover your own proofs. Is the hypothesis necessary? Is the converse true? What happens in the classical special case? What about the degenerate cases? Where does the proof use the hypothesis? »
- Godfrey Harold Hardy (1877 - 1947)
- « The mathematician’s patterns, like the painter’s or the poet’s must be beautiful; the ideas like the colours or the words, must fit together in a harmonious way. Beauty is the first test: there is no permanent place in the world for ugly mathematics. »
- John von Neumann (1903 - 1957)
- «If people do not believe that mathematics is simple, it is only because they do not realize how complicated life is. »
-
- « Young men should prove theorems, old men should write books. »
- Hermann Weyl (1885 - 1955)
- « My work always tried to unite the truth with the beautiful, but when I had to choose one or the other, I usually chose the beautiful. »
- Edward Brian Davies (1944 -)
- « Studying non-self-adjoint operators is like being a vet rather than a doctor: one has to acquire a much wider range of knowledge, and to accept that one cannot expect to have as high a rate of success when confronted with particular cases. It comprises a collection of methods, each of which is useful for some class of such operators. »
- Daniel W. Stroock (1940 -)
- « Mathematics is one, and possibly the only, human endeavor for which there is a widely, if not universally, recognized criterion with which to determine truth. For this reason, mathematicians can avoid some of the interminable disputes which plague other fields. On the other hand, I sometimes wonder whether the most interesting questions are not those for which such disputes are inevitable. »
- Terence Chi-Shen Tao (陶哲軒) (1975 - )
- Sir William Timothy Gowers (1963 - )
- William P. Thurston (1946 - )
- Others
- Georges Brassens (1921 - 1981)
- « Mais sans technique, un don n'est rien ♫ Qu'une sale manie… » in Le mauvais sujet repenti
- Antonio Gramsci (1891 - 1937) (also attributed to Romain Rolland)
- « I’m a pessimist because of intelligence, but an optimist because of will. » in Letter from Prison (19 December 1929);
- Audrey Dussutour (1977 - )
- « La recherche est comme une plante, dont la fleur serait la recherche appliquée, et la racine la recherche fondamentale. »
- Some curiosities
- How to select the number of classes in a histogram? Californian way and Parisian way
- Money
- Who said that mathematicians do not like money? It seems at least that the converse is false…