Djalil CHAFAÏ (شافعي جليل)

• CEREMADE • Université Paris-Dauphine - PSL • Place du Maréchal de Lattre de Tassigny, 75775 Paris Cedex 16
• DMA • École normale supérieure (Paris) - PSL • 45 rue d'Ulm, 75230 Paris Cedex 5
• Email. firstname@lastname.net (without diacritics)
• Blog. Libres pensées d'un mathématicien ordinaire

• Geometric and probabilistic functional analysis, concentration, convexity, isoperimetry
• Random matrices, random graphs, random tensors, free probability, and high dimensional phenomena
• Convexity and positivity, variational analysis, potential theory
• Asymptotic analysis, exact solvability, special functions
• Stochastic models and stochastic inverse problems:
  • Mathematical Biology (pharmacology, biostatistics)
  • Mathematical Physics (spin systems, interacting particle systems, statistical physics)
  • Data Science (data streams processing, queuing, machine learning, decision making)
  • Earth Science (variational assimilation in meteorology)
• Random structures and algorithms, stochastic simulation
• Markov processes/semigroups, their equilibrium/geometry
• Sobolev type inequalities and partial differential equations
• Poisson and Gauss measures, heat kernels, limit theorems
• Boltzmann-Shannon and Voiculescu entropies, information theory, operator theory

Algebraic/geometric rigidity in analysis and probability.

Some pictures illustrating my research, created mostly with Octave, Python, or Julia. Enjoy visual mathematics!

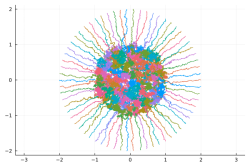
• Left: Spectrum of a high dimensional square matrix with heavy tailed (infinite variance) iid entries:
  Right: Voronoi cells of the spectrum of a high dimensional matrix with iid Gaussian entries:
  
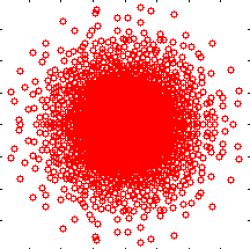
  More in arXiv:1006.1713 and in arXiv:1109.3343
• Trajectories of an eight particles Hamilton-Monte-Carlo algorithm for a one-dimensional log-gas:
  
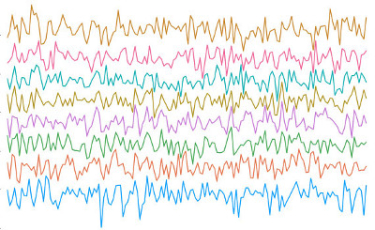
  More in arXiv:1806.05985
• Phase portrait of the reciprocal polynomial of the characteristic polynomial of a high dimensional Gaussian matrix (left: complex, right: real):
  
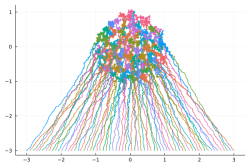
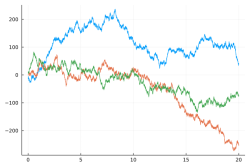
  More in arXiv:2012.05602 and Blogpost
• Left: three independent real Brownian motion (time in horizontal axis):
  Center: the same BMs with a quadratic confinement making them three independent Ornstein-Uhlenbeck (OU) processes:
  Right: the same OUs with singular repulsion making them a single three particles Dyson-Ornstein-Uhlenbeck process:
  
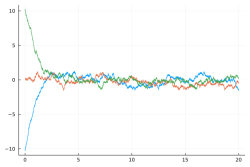
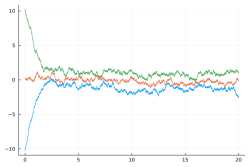
  More in arXiv:2107.14452 Talk slides
• Trajectory of a planar Dyson Ornstein-Uhlenbeck process with 66 particles started from a uniform grid on circle or line:
  
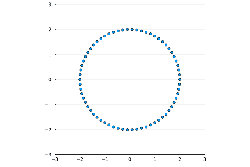
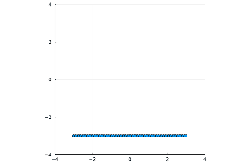
  Click on picture to see animation. More in arXiv:1706.08776 and in Blogpost
• The same data displayed statically:
  
  More in arXiv:1706.08776 and in Blogpost
• Equilibrium measures of planar Coulomb gas with various conditionings on linear statistics:
  
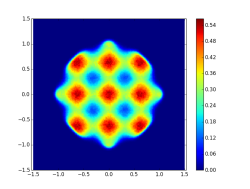
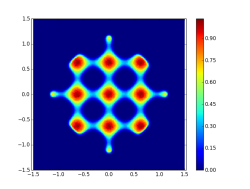
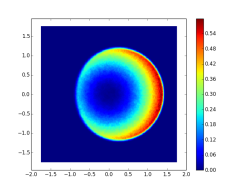
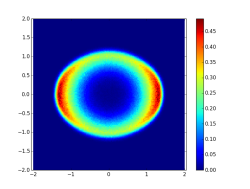
  These pictures are courtesy of my co-author Grégoire Ferré. More in arXiv:1907.05803
• Equilibrium measure in dimension $4$ for $\log\left\Vert\cdot\right\Vert_2$ repulsion and $\left\Vert\cdot\right\Vert_4^4$ confinement, projected on first three coordinates:
  
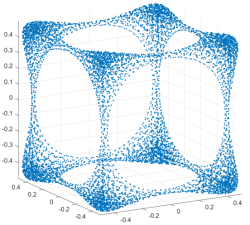
  This picture is courtesy of my co-author Robert S. Womersley. More in arXiv:2206.04956
• Sample of the Green field on the two-sphere with the chardal gas $\{(L_n(g_p))\}_{p\in\mathbb{S}^2}$ with $n = 5000$ particles:
  
  More in arXiv:2606.00330 and arXiv:2510.18669

• Current doctoral students
  • Samuel Chan-ashing (2024-, Paris-Dauphine - PSL, with Quentin Cormier)
    Long time behavior of diffusion processes : cutoff phenomenon and metastability
  • Rémi Bonnin (2024-, Aix-Marseille Université, with Charles Bordenave)
    High dimensional random tensors
  • Kewei Pan (2023-, Toulouse, with Guillaume Cébron, main advisor)
    Around Boolean entropy, random matrices, and Coulomb gases
• Current postdoctoral researchers
  • Ronan Mémin (2025-2028, with Laure Dumaz, SPAM)
    Random matrices, Beta-ensembles
• Former postdoctoral researchers
  • Guillaume Dubach (2022-2023, FSMP)
    Probability theory, especially random matrices
    Actuellement professeur Monge à l'École polytechnique
• Former doctoral students on Mathematical genealogy project
  • Quentin François (Paris-Dauphine - PSL 2025, with Pierre Tarrago)
    Random Matrices : high dimension and exact solvability
    Actuellement post-doctorant à l'Université de Lille avec Rémi Bardenet et Raphaël Butez
  • Hugo Magaldi (Paris-Dauphine - PSL 2022, with Laure Dumaz, main advisor)
    Étude des beta-ensembles et leur limite à haute température
    Actuellement ingénieur
  • Jeanne Boursier (Paris-Dauphine - PSL 2022, with Sylvia Serfaty)
    Quelques problèmes de mécanique statistique pour les gaz de Coulomb et de Riesz
    Presently Postdoctoral fellow, J.F. Ritt Assistant Professor, Columbia University, New York
  • Josué Corujo (Paris-Dauphine - PSL 2021, with Simona Grusea)
    Multi-allelic Moran models and quasi-stationary distributions
    Actuellement maître de conférences à l'Université Paris-Est Créteil
  • Ezéchiel Kahn (École des Ponts ParisTech 2021, with Benjamin Jourdain)
    Matrices de covariance : diffusions, probabilités libres, et apprentissage profond
    Actuellement haut fonctionnaire du Corps des Ponts, des Eaux, et des Forêts
  • David García-Zelada (Paris-Dauphine - PSL 2019)
    Aspects géométriques et probabilistes des gaz de Coulomb
    Actuellement maître de conférences à Sorbonne Université
  • Raphaël Butez (Paris-Dauphine - PSL 2017)
    Polynômes aléatoires, gaz de Coulomb, et matrices aléatoires
    Actuellement maître de conférences à l'université de Lille
  • Marie-Noémie Thai (Marne-la-Vallée / Paris-Est 2015, with Amine Asselah)
    Processus de Fleming-Viot, distributions quasi-stationnaires et marches aléatoires en interaction de type champ moyen
    Actuellement enseignante à l'École supérieure d'ingénieurs Léonard-de-Vinci
  • Bertrand Cloez (Marne-la-Vallée / Paris-Est 2013)
    Comportement asymptotique de processus avec sauts et applications pour des modèles avec branchement
    Actuellement directeur de recherches à l'INRAE
  • Julie Champion (Toulouse 2013, with Franck Barthe)
    Sur les algorithmes de projection en entropie relative avec contraintes marginales
    Actuellement professeure en classes préparatoires aux grandes écoles
  • Julie Antic (Toulouse 2009, with Didier Concordet)
    Nonparametric methods for population PK and/or PD
    Actuellement ingénieure dans l'industrie spatiale
    

Quelques activités d'animation dans le cadre du milieu professionnel mais en dehors de l'enseignement et de la recherche canoniques :

• Après-midi des lycéens à l'ÉNS 2026 (conception et organisation)
• Après-midi des lycéens à l'ÉNS 2025 (conception et organisation)
• Après-midi des lycéens à l'ÉNS 2024 (participation en tant qu'orateur)
• Journées ÉNS - CPGE 2025 - Autour du prix Abel de Michel Talagrand (conception et organisation)
• Journées ÉNS - CPGE 2024 - Géométries (conception et organisation)
• Journées ÉNS - CPGE 2023 - Autour des médailles Fields 2022 (conception et organisation)
• PSL Week 2023 : Modéliser le monde réel, pratiques et limites (conception et organisation)
• Week-end DMA 2024 - Le Tréport et Amiens (conception et organisation)
• Week-end DMA 2023 - Étretat et Jumièges (conception et organisation)

• Séminaire Matrices Et Graphes Aléatoires (MEGA) - Institut Henri Poincaré
• Séminaire informel de probabilités du DMA - École normale supérieure
• Projet et séminaire Automath

Underlined item if participation to the organization or scientific committee. Standard seminars/colloquiums are not listed.

• 2028-T1. Topics between Statistical Physics and Mathematics - Talking across fields (IHP Paris, with Guillaume Barraquand and Cristina Toninelli)
• 2027-T2. High Dimensional Probability and Analysis, Continuous and Discrete (IHP Paris)
• 2026-12. Journée scientifique autour des prix de l'Académie des sciences en mathématiques (ÉNS Paris)
• 2026-08. Frontiers in Random Matrix Theory and Applications (Tianyuan Mathematics Research Center, Kunming)
• 2026-07. Characteristic Polynomials (Institute Mittag-Leffler Djursholm, with Gaultier Lambert and Ashkan Nikeghbali)
• 2026-06. Random Matrices (Mathematisches Forschungsinstitut Oberwolfach)
• 2026-05. Recent Progress on Self-Interacting Processes and Non-Reversible Monte Carlo (École normale supérieure - PSL)
• 2026-05. Point configurations : from statistical physics to potential theory (CIRM Luminy, with Dmitriy Bilyk, Peter Grabner, and Sylvia Serfaty)
• 2026-03. Entropy and Random Matrices (CIRM Luminy)
• 2026-01. Journées de Statistique Mathématique 2026 (Orsay)
• 2025-07. International Research Network France-Korea (Bordeaux)
• 2025-06. ANR Conviviality meeting between probability theory and analysis of partial differential equations (Lyon)
• 2025-06. Workshop on Functional Inequalities (Paris-Dauphine)
• 2025-05. Constructive Functions 2025 - Celebrating Ed Saff’s 80th birthday (Nashville)
• 2025-03. Journées Louis Antoine 2025 (Rennes, avec Pierre Tarrago)
• 2025-03. Kick-off meeting - Cross Disciplinary Project C2EMPI (Lille)
• [Archive] 2020-05. Random Matrices and their Applications (New York) < Covid-19 - Onlined
• [Archive] 2019-07. PSL/CNRS summer school on high dimensional probability and algorithms (ENS Paris)
• [Archive] 2018-05. Random Matrices and their Applications (Kyoto)
• [Archive] 2018-05. Concentration of measure and its applications (Cargèse)
• [Archive] 2017-12. Journée algorithmes stochastiques à Paris-Dauphine (Paris-Dauphine)
• [Archive] 2016-06. Optimal and random point configurations: from statistical physics to approximation theory (IHP Paris)
• [Archive] 2015-06. Journée CEREMADE-LAMSADE-LEDa 2015 (Paris-Dauphine)
• [Archive] 2015-01. Workshop on random matrices and their applications (Hong Kong)
• [Archive] 2014-12. États de la recherche en matrices aléatoires (IHP Paris)
• [Archive] 2014-08. Journées MAS 2014 (Toulouse)
• [Archive] 2014-03. Recent advances on log-gases (IHP Paris)
• [Archive] 2014-03. Journée Hawkes à Paris-Dauphine (Paris-Dauphine)
• [Archive] 2013-05. School on threshold phenomena and random graphs (IHP Paris
• [Archive] 2012-10. Workshop on random matrices and their applications (Telecom Paris)
• [Archive] 2012-03. Journées Processus de Markov Déterministes par Morceaux (Marne-la-Vallée)
• [Archive] 2011-06. School on random matrices, stochastic geometry, and compressed sensing (IHP Paris)
• [Archive] 2010-05. Workshop on Probability and Geometry in High Dimensions (Marne-la-Vallée)
• [Archive] 2009-11. Fall School on compressed sensing, random matrices, high dim. geometry (Marne-la-Vallée)
• [Archive] 2008-06. Journées Statistiques du Sud 2008 (Toulouse)

Only running collaborative projects :

• Matrices Et Graphes Aléatoires (MEGA) funded by CNRS
• Conviviality (Convergence et interactions via Analyse et Probabilités) funded by ANR
• TAGADA (Tenseurs aléatoires en grande dimension et applications) funded by ANR
• Statistical Physics and Mathematics - SP(A)M! - Funded by PSL and linking Dauphine/CEREMADE, ENS/DMA, and ENS/LPENS

You may read Publications: science, money, and human comedy on my blog.

Digital footprint in professional data bases :

• arXiv and Hyper Article en Ligne
• Google Scholar, and Semantic Scholar
• MathSciNet, zbMATH, and ORCID

Partial list of publications automatically provided by arXiv :

• Topics in statistical mechanics
  With Ewain Gwynne, Nina Holden, Xin Sun, Arnaud Le Ny, Sébastien Ott, Yvan Velenik, Rémi Rhodes, Vincent Vargas
  Edited by Cédric Boutillier, Béatrice de Tilière, Kilian Raschel
  Panoramas et Synthèses 59, Société Mathématique de France (SMF), (2023) 229p.
  Chapter on arXiv
  
• Modern Aspects of Random Matrix Theory
  With Charles Bordenave; Alice Guionnet; Alan Edelman, Brian Sutton, Yuyang Wang; Mark Rudelson; Terence Tao, Van Vu (Editor)
  Proceedings of Symposia in Applied Mathematics (PSAPM) 72 American Mathematical Society (AMS), (2014) 172p.
  
• Interactions between compressed sensing, random matrices, and high dimensional geometry
  With Olivier Guédon, Guillaume Lecué, and Alain Pajor
  Panoramas et Synthèses 37, Société Mathématique de France (SMF), (2012) 182p.
  Draft (PDF) · Errata (PDF)
  
• Sur les inégalités de Sobolev logarithmiques (in French)
  With Cécile Ané, Sébastien Blachère, Pierre Fougères, Ivan Gentil, Florent Malrieu, Cyril Roberto and Grégory Scheffer
  With a preface by Dominique Bakry and Michel Ledoux
  Panoramas et Synthèses 10, Société Mathématique de France (SMF), (2000) xvi+217p.
  Photo of S.O. Bologs · Private access for sobologs
  Preface · Errata (PDF) · Expanded first chapter on HAL
  

• Advanced Topics in Random Matrices
  Proceedings of the États de la recherche 2014, Société Mathématique de France, held in Institut Henri Poincaré, Paris.
  By Florent Benaych-Georges, Charles Bordenave, Mireille Capitaine, Catherine Donati-Martin, Antti Knowles
  Edited by Florent Benaych-Georges Djalil Chafaï, Sandrine Péché, and Béatrice de Tilière
  Panoramas et Synthèses 53, Société Mathématique de France (SMF), (2018) xii+204p.
  
• Covid-19 | Regards croisés sur la crise
  Recueil de textes pluridisciplinaires rassemblés par Bruno Bouchard et Djalil Chafaï
  Éditions électroniques de l'Université Paris-Dauphine - PSL, 113p (2021)
  

• Aléatoire (dont une introduction aux matrices aléatoires)
  En collaboration avec Sylvie Méléard et Christophe Giraud
  Actes des journées X-UPS 2013
  Édités par Pascale Harinck, Alain Plagne, et Claude Sabbah
  Éditions de l'École Polytechnique (2013) 122p.
  Livre (papier ou PDF) · Exposé (PDF) · Questions/réponses (Blog)
  
• Modélisation stochastique et simulation (cours et applications)
  En collaboration avec Bernard Bercu
  Mathématiques appliquées pour le Master - Collection Sciences Sup
  Société de Mathématiques Appliquées et Industrielles (SMAI)
  Éditions Dunod (2007) 352p.
  Errata (PDF) · Codes (ZIP)
  
• Recueil de modèles aléatoires
  En collaboration avec Florent Malrieu
  Collection Mathématiques & Applications Volume 78 Société de Mathématiques Appliquées et Industrielles (SMAI)
  Éditions Springer (2016) XIII+398p (Mathematical Reviews)
  ISBN 978-3-662-49767-8 (Print) 978-3-662-49768-5 (Online)
  Version papier et électronique chez Springer et version électronique sur libgen
  Rappels de cours (43p) + errata version Springer + codes (Julia, Octave, Python, Scilab)
  Version électronique auteurs post-publication sur HAL
  
• Probabilités - Préparation à l'agrégation interne
  En collaboration avec Pierre-André Zitt
  Auto-édition, version électronique gratuit et version papier vendue à prix coûtant (163p.)
  Version électronique en couleur disponible gratuitement sur HAL, éditions 2016, 2017, 2020
  Version papier noir & blanc vendue à prix modique et coûtant (<5€) sur Amazon France, éditions 2016, 2020 :
  

• Aspects of the spherical ensemble
  Talk slides (Oberwolfach Workshop “Random Matrices”, 2026) : PDF
• Selected topics around the concentration of measure
  Lecture notes for a minicourse (Learning (and) statistics with Talagrand, Journées de Statistique Mathématique, Orsay 2026) : PDF
• Aspects of the Cutoff Phenomenon for Diffusions
  Talk slides (Séminaire du CMAP, École Polytechnique, Palaiseau, 2025) : PDF
• Autour de la théorie de l'information
  Exposé pour un après-midi mathématique à destination des lycéens, École normale supérieure, Paris, 2024) : PDF
• Mini-course on logarithmic Sobolev inequalities
  Lecture notes (MEGA@IHP and DMA@ÉNS, Paris, April and December 2024) : PDF
• Riesz Energy Problems and Integral Identities - Unexpected phenomena for equilibrium measures
  Talk slides (Paris, 2022) : PDF
• Dyson Ornstein Uhlenbeck process : cutoff phenomenon
  Talk slides (Bielefeld-Melbourne, 2022) : PDF
  Talk slides (Sorbonne Université - IMJ AF, 2022) : PDF
• Probabilités, analyse, et physique statistique
  Talk slides (ÉNS, 2021) : PDF
• About random matrices
  Talk slides (Stanford, 2021) : PDF
• Aspects of Coulomb gases
  Talk slides (Oberwolfach, 2019) : PDF
• Dynamics of a planar Coulomb gas
  Video capture (Providence, 2018) : Stream
• Matrices aléatoires
  Video capture (Orsay, 2016) : Stream
• Au bord de certains systèmes de particules en interaction issus ou inspirés par des modèles de matrices aléatoires
  Video capture (Collège de France, 2016) : Stream
• About non-Hermitian random matrices
  Talk slides (Cargèse, 2014) : PDF
• About confined particles with singular pair repulsion
  Talk slides (Toulouse, 2014) : PDF
• The circular law
  Talk slides (San Diego, 2013) : PDF
• Graphes et matrices aléatoires - Quelques aspects
  Planches d'exposé MAP-432 (École Polytechnique, 2012) : PDF
• Matrices aléatoires - Quelques aspects
  Planches d'exposé (Marne-la-Vallée, 2011) : PDF
• Autour du théorème limite central
  Planches d'exposé (Marne-la-Vallée, 2011) : PDF

• Processus des restaurants chinois et loi d'Ewens
  Écrit avec Yan Doumerc et Florent Malrieu
  Paru dans RMS ex Revue de Mathématiques Spéciales, vol. 123 n°3 (2013)
  Article : PDF

These documents are (un)published in the prestigious Journal of Unpublished Results. I have not tried viXra for the moment.

• About the spectral analysis of large random Markov kernels
  Talk notes (2012) : PDF
• Quelques mots sur l'inégalité de concentration de Azuma-Hoeffding
  Notes d'exposé (2012) : PDF
  Planches d'exposé (2014) : PDF
• Singular values of random matrices
  Rough lecture notes (2009) : PDF
• Dimension d'entropie, d'après Guionnet and Shlyakhtenko
  Notes d'exposé (2008) : PDF
• Questions/réponses simples de calcul stochastique
  Notes pédagogiques (2008) : PDF
• Random projections, marginals, and moments
  Rough expository notes (2007) : PDF
• Inégalités de Poincaré et Gross pour mesures de Bernoulli, Poisson, et Gauss
  Notes d'exposition (2005) : HAL
• Quelques mots sur l'entropie
  Notes incomplètes (2002, 2005) : PDF
• Sur certaines mesures produit conditionnées
  Notes d'exposé (2005) : PDF
• Covariance de modèles d'interface et marches aléatoires en environnement aléatoire
  Notes d'exposé (2002) : PDF
• Un petit peu de grandes déviations
  Exposé au séminaire étudiant (1999) : PDF
  C'est lors de cet exposé qu'a germé l'idée d'écrire un livre collectif sur les inégalités de Sobolev logarithmiques, en suivant l'exemple du mémoire collectif « Grandes déviations sans larmes » écrit par des doctorants du laboratoire quelques années plus tôt. Notre projet a pris forme en février 1999, par un exposé, le premier d'une liste de dix, au groupe de travail du laboratoire. Le premier jet de notre manuscrit collectif était dans nos valises lors de l'école d'été de Saint-Flour 1999 ! S'en est suivi un long travail et maintes péripéties…
• Elementary proof of inequalities on paths space for Lévy processes
  Short note (2002) : PDF
• Covariance matrices with prescribed null entries
  In collaboration with Didier Concordet
  Rough technical report (2006) : PDF
• A note on functional inequalities for some Lévy processes
  In collaboration with Florent Malrieu
  Short note (2002) : PDF
  Extended by Ivan Gentil and Cyril Imbert in two published papers: (2008) HAL1 and (2009) HAL2
• Contributions à l'étude de modèles biologiques, d'inégalités fonctionnelles, et de matrices aléatoires
  Mémoire d'habilitation à diriger des recherches (2008) : Thèse en ligne
• Sur les inégalités de Sobolev logarithmiques en théorie de l'information et pour des systèmes de spins conservatifs en mécanique statistique
  Mémoire de Doctorat (2002) : Thèse en ligne
• Grandes déviations pour la mesure empirique sur un champ de Gibbs
  Mémoire de DEA (1997) : PDF

• Vice-présidence du numérique : 2017-2020
  Billet de blog daté de décembre 2020
• Modélisation et analyse quantitative
  Billet de blog daté de novembre 2020
• Modelling
  Blog post dated May 2020
• Formation à distance
  Billet de blog daté de mars 2020
• Paris-Dauphine : coronavirus et numérique
  Billet de blog daté de mars 2020
• Franchise universitaire et droit de grève
  Billet de blog daté de mars 2020
• Numér'hic
  Billet de blog daté de mars 2020 sur le moteur de recherche Qwant et le numérique éthique
• Annals of mathematics: probability and statistics
  Blog post dated November 2019
• How to give a bad talk
  Blog post dated September 2018
• Office 365
  Billet de blog daté de décembre 2017 sur le bouquet de services Office365 à Paris-Dauphine
• Lutte des classes et domination sociale
  Billet de blog daté d'avril 2017 sur le monde universitaire
• Réflexions sur les frais d’inscription en licence à l’université
  Billet de blog daté d'octobre 2016 sur les frais d'inscriptions à l'Université
• Dauphine : frais de scolarité
  Billet de blog daté de janvier 2016 sur les frais de scolarité à Paris-Dauphine
• Triangles
  Billet de blog daté de décembre 2013 sur le positionnement scientifique
• Starting point and curiosity
  Blog post dated June 2010
• Publications: science, money, and human comedy
  Blog post dated January 2012
• Mathématiques de l'aléatoire et physique statistique
  Contribution au livre de la recherche pour les cinquante ans de Paris-Dauphine (2018)
  Version en ligne (billet de blog)
• Mathématiques, probabilités, algorithmes
  Texte d'introduction à un texte de Pierre Monmarché, lauréat du Prix du Monde de la recherche 2015.
  Paru aux Éditions Le Pommier dans un recueil consacré au Prix.
  Version en ligne (billet de blog)
• Coût des publications : propositions concrètes
  Paru dans Gazette des Mathématiciens 139 Société Mathématique de France (SMF) (2014) 82-86 PDF
  Paru dans Matapli 103 (2014) 85-90 Société de Mathématiques Appliquées et Industrielles (SMAI) PDF
  Version en ligne (billet de blog)
• Coût des publications : un exemple instructif
  Paru dans Gazette des mathématiciens 137 Société Mathématique de France (SMF) (2013) 119-122 PDF
  Lire également EJP-ECP: twenty years of freeness (billet de blog)

Ce que l'on conçoit bien s'énonce clairement et les mots pour le dire arrivent aisément.
Nicolas Boileau, L'art poétique (1674) Chant I.
J'ajouterais quant à moi que la réciproque n'est pas forcément juste. Méfiez vous des beaux parleurs !

• PDF 2026-2027 Notes de cours (~141p.)
• PDF 2025-2026 Partiel avec éléments de solution
• PDF 2025-2026 Examen avec éléments de solution
• PDF 2024-2025 Partiel avec éléments de solution
• PDF 2024-2025 Examen avec éléments de solution

• PDF 2023-2024 Notes de cours (~120p.)
• PDF 2022-2023 Examen sans correction
• PDF 2022-2023 Examen avec correction
• PDF 2023-2024 Examen avec correction

• PDF 2024-2025 Notes de cours (~94p.)

A pre-school week for second year of Master Mathématiques de l'Assurance de l'Économie et de la Finance (MASEF) and Master Mathématiques Appliquées et THéoriques (MATH). The objective of this pre-school is to recall fundamental aspects of probability theory at the level of a first year of master. This helps to prepare the students for the courses proposed in the master in particular to the course on stochastic calculus. Before the year 2021–2022, this pre-school was essentially the first part of the stochastic calculus course. What was removed (actually postponed to the stochastic calculus course) is the Lebesgue – Stieltjes integral associated to paths of finite variation, the Wiener integral, the Cameron-Martin formula, and its application to exit times, and the Kunita-Watanabe inequality.

• PDF 2021-2022 Rough lecture notes with typos (~65p.)
• Some historical documents around Brownian motion and stochastic calculus
• Petit billet de blog, en français
• Short bibliography:
  • Borkar - Probability theory. An advanced course (1995)
  • Gut - Probability: a graduate course (2013)
  • Revuz and Yor - Continuous martingales and Brownian motion (1999)

This course belongs to the Master Mathématiques de l'Assurance de l'Économie et de la Finance (MASEF) and Master Mathématiques Appliquées et THéoriques (MATH). It provides an introduction to stochastic calculus: Brownian motion, quadratic variation, Doob stopping and maximal inequalities for martingales, local martingales, stochastic integral, semi-martingales, Itô formula, Lévy characterization of Brownian motion, Girsanov formula, Dubins-Schwarz theorem, stochastic differential equations with Lipschitz coefficients, notion of explosion for locally Lipschitz coefficients, Bessel, Ornstein-Uhlenbeck, and Langevin processes, Markov semigroup and infinitesimal generator, Duhamel formula, strong Markov property, link with Fokker-Planck and heat partial differential evolution equations, Feynman-Kac formula and real Schrödinger operators, probabilistic representation of the Dirichlet problem.

• PDF 2020-2021 Rough lecture notes with typos (~150p.)
• PDF 2020-2021 Exam without solutions
• PDF 2020-2021 Exam with solutions
• PDF 2019-2020 Exam without solutions
• PDF 2019-2020 Exam with solutions
• PDF 2018-2019 Exam without solutions
• PDF 2018-2019 Exam with solutions
• Some historical documents around Brownian motion and stochastic calculus
• Petit billet de blog, en français
• Short bibliography:
  • Baudoin - Diffusion Processes and Stochastic Calculus, EMS (2014)
  • Evans - An introduction to stochastic differential equations, AMS (2013)
  • Le Gall - Brownian Motion, Martingales, and Stochastic Calculus, Springer (2016)
  • Ikeda and Watanabe - Stochastic Differential Equations and Diffusion Processes, North-Holland (1981)
  • Karatzas and Shreve - Brownian Motion and Stochastic Calculus, Springer (1988)
  • Kuo - Introduction to Stochastic Integration, Springer (2005)
  • Øksendal - Stochastic Differential Equations: An Introduction with Applications, Springer (2010)
• Archive before 2017 from Halim Doss, vintage, hand written, in French
  • PDF notes de cours (~90p.)
  • PDF énoncés des exercices sans correction (~70p.)

This course, in collaboration with Joseph Lehec, belonged to the Master Mathématiques Appliquées et THéoriques (MATH). This course provides a modern overview on logarithmic Sobolev inequalities. These inequalities have been the subject of intense activity in the recent decades in relation with the analysis and geometry of Markov processes and diffusion evolution equations. This course is designed to be accessible to a wide audience. It is divided into seven lectures. The examination will consist in reading a research paper in the field and giving a short talk on it.

This course was also given in Universidad de Chile, Santiago de Chile, in fall 2017, as part of the Programme Régional France - Amérique latine Caraïbe (PREFALC) organized by Stéphane Mischler.

• PDF 2017-2018 Rough lecture notes (~76p.)
• Short bibliography:
  • D. Bakry & I. Gentil & M. Ledoux - Analysis and Geometry of Markov Diffusion Operators
  • G. Royer - An Initiation to Logarithmic Sobolev inequalities
  • C. Ané et al - Sur les inégalités de Sobolev logarithmiques

• MAP-311 (Introduction aux probabilités)
  • PDF 2016-2017 Exercices (~90, 20p.)
  • PDF 2016-2017 Exercices corrigés (~90)
  • PDF 2016-2017 Projet Estimation du paramètre d'une loi exponentielle
  • PDF 2016-2017 Projet Estimateur par fenêtres glissantes
  • PDF 2015-2016 Projet Marche aléatoire sur le cercle
  • PDF 2015-2016 Projet Permutations aléatoires
  • PDF 2014-2015 Projet Modèle de Wright-Fisher
  • PDF 2014-2015 Projet Agrégation limitée par diffusion interne
  • PDF 2013-2014 Projet Marche aléatoire en paysage aléatoire
  • PDF 2012-2013 Projet Équation de récurrence linéaire sur un signal
  • PDF 2012-2013 Projet Simulation de lois discrètes
  • PDF 2012-2013 Projet Modélisation et simulation d'une revue
  • PDF 2011-2012 Projet Matrices doublement stochastiques
  • PDF 2011-2012 Projet Permutations aléatoires
  • PDF 2011-2012 Projet Approximations gaussienne et poissonnienne
  • PDF 2011-2012 Projet Processus de taille de fenêtre TCP
• MAP-432 (Markov et Martingales)
  • PDF 2013-2014 Note à propos des trucs probabilistes élémentaires
  • PDF 2013-2014 Note à propos d'une LGN et d'un TCL randomisés
  • PDF 2013-2014 Note à propos des chaînes de Markov discrètes
  • PDF 2013-2014 Note à propos des temps d'atteinte pour les chaînes de Markov discrètes
  • PDF 2011-2012 Exposé Graphes et matrices aléatoires

Ce cours faisait partie du Master 1 Mathématiques Appliquées de Dauphine-PSL.

• PDF 2016-2017 Notes de cours avec coquilles (102p.)
• PDF 2016-2017 Exercices de travaux dirigés avec correction (52p.)
• PDF 2016-2017 Annales d'examens avec correction (72p.)
• PDF 2016-2017 Livret (tout en un : notes de cours, exercices et annales corrigés) (228p.)

Ce cours faisait partie du Master Mathématiques appliquées - Parcours Analyse et Probabilité. Il a été dispensé (en anglais) pour la dernière fois en 2014-2015. Les notes de cours ci-dessous sont en français.

This course is divided into 7 lectures of 3 hours. Each lecture is devoted to the study of a particular stochastic model. The selected models may vary from one year to another, and the selection for 2013 included Fisher-Wright models, Random walks models, Galton-Watson branching models, Random matrix models, and Growth-fragmentation models. The examination consists in giving a mini-lecture on an article in the spirit of the course. The course is in English, and some lecture notes in French are available below.

• PDF 2013-2014 Notes de cours (109p.) (ancêtre du livre Recueil de modèles stochastiques avec Florent Malrieu)
• PDF 2012-03 Examen mars 2012 Marne (processus de branchement sexué, modèle de Daley)
• PDF 2011-03 Blog Examen mars 2011 Marne (problème de la plus longue sous-suite croissante)

• PDF 2007 Notes de cours (113p.) en collaboration avec Florent Malrieu
• PDF 2007 Examen Rennes
• PDF 2007 Examen Rennes (Corrigé)
• PDF 2007 Examen Toulouse
• PDF 2007 Examen Toulouse (Corrigé)
• PDF 2008 Examen Toulouse
• PDF 2010 Examen Marne-la-Vallée

Le cours de Biskra (2006) a été donné en marge d'un colloque sur l'analyse stochastique et ses applications, organisé principalement par Brahim Mezerdi (Université de Biskra) et Boualem Djehiche (KTH Stockholm). Biskra est une ville des Aurès, aux portes du Sahara, dans l'est algérien. Le cours d'Oran (2011) a été donné conjointement avec Amine Asselah, à l'invitation de Setti Ayad (Université d'Oran), pour des étudiants de master d'Oran et de Tlemcen.

• PDF Biskra 2006 Notes de cours (57p. rédigées par DC)
• PDF Oran 2011 Notes de cours de Ferrari et Galves
• PDF Oran 2011 Livre de D. A. Levin-Peres-Wilmer
• PDF Oran 2011 Feuille d'exercices (rédigée par AA)
• PDF Oran 2011 Exemple de convergence abrupte (rédigé par DC)

Des notes de cours rédigées en collaboration avec Pierre-André Zitt, sous forme de livre, sont disponibles ci-dessus.

• PDF 2013 Résumé sur le phénomène du biais par la taille
• PDF 2013 Résumé sur les convergences

Ce matériel date de la période 1999-2002, 2003-2005.

• PDF Fragment n°0 - Une initiation à Matlab
• PDF Fragment n°1 - Qu'est-ce que la simulation ?
• PDF Fragment n°2 - Théorèmes limites classiques
• PDF Fragment n°7 - Quelques mots sur l'entropie
• PDF Appendice - Quelques lois classiques
• PDF Feuille de TP n°1 - Initiation Matlab
• PDF Feuille de TP n°2 - Initiation Matlab
• PDF Feuille de TP n°3 - LGN et TLC
• PDF Feuille de TP n°4 - Calcul d'intégrales par méthode de Monte-Carlo
• PDF Feuille de TP n°5 - Espérance conditionnelle en modélisation
• PDF Feuille de TP n°6 - Martingales en modélisation
• PDF Feuille de TP n°7 - Vecteurs aléatoires et modèle linéaire gaussiens
• PDF Feuille de TP n°8 - Tests non paramétriques du chi-deux en modélisation
• PDF Feuille de TP n°9 - Régions de confiance en modélisation
• PDF Feuille de TP n°10 - Fonction de répartition empirique
• PDF Feuille de TP n°11 - Loi exponentielle en modélisation
• PDF Feuille de TP n°12 - Chaînes de Markov à espace au plus dénombrable
• PDF Feuille de TP n°13 - Transformée de Laplace en modélisation
• PDF 2002 Vieux manuel (140p.)

• PDF Texte sur un modèle d'agrégat écrit par Sébastien Blachère (Université de Marseille)
• PDF Texte sur Kaplan-Meier écrit par Jean-François Dupuy (Université de Toulouse III)
• Informations en provenance du jury du concours

• M@ths en Ligne
• Cours en ligne (CEL)
• Dimension et Chaos
• The Visual Math Institute
• Image des mathématiques

• Blog posts speaking about…
  Julia, Emacs, Linux
• Simcoul Julia code
  In collaboration with Grégoire Ferré
  Julia code for simulation of Coulomb gases and more with HMC
  Git repository on CNRS/PLM GitLab
• The w2m.py Python module/script
  Python web spider walking through a subset of WWW and producing an adjacency matrix
  Module on PyPi Git repository on GitHub
• The ejpecp LaTeX2_ε class
  In collaboration with Krzysztof Burdzy
  LaTeX2_ε document class for Electronic Journal of Probability and Electronic Communications in Probability
  LaTeX Package on CTAN
• Computational Rough Paths (CoRoPa)
  In collaboration with Terry J. Lyons
  C++ template classes libraries handling tree structures and free Lie algebras, including Campbell-Baker-Hausdorff formula, shuffle product, Dynkin map, dynamic Hall bases, etc. Based on STL and compatible with GMP
  Webpage and package on SourceForge
• The Girko circular law in Python via SageMathCell
  

You said Miscellany?

• Read and write my name
  • On my passports and ID cards, my name is written Djalil Chafaï
  • Read Djalil like you read it in Django Reinhardt (thanks Jack!)
  • Djalil is my first name and Chafaï is my surname or lastname or family name
  • English speaking people should read my name as Jalil Shaf-i-e
  • French speaking people should read it as Djè-lil Chaf-aille-i
  • Arabic speaking people may read it directly شاﻓﻌﻲ جلیل
  • All the rest of the world may read IPA ʃaːfɪʕɪ dʒəlɪl
  • Maybe I will try with berber's Tifinagh or MP3
  • For (La)TeX you may write Djalil Chafa\“{\i}
  • For ArabTeX you may use ^sAfi`iy ^galiyl
  • For HTML just write Djalil Chafaï
  • For xML you may use arabic unicode or IPA unicode
• Numbers
  • Favourite prime number is 15061973, the 974461^th
  • Asymmetric cryptographic public key is here
  • Mathematical Reviews Author ID is 653638
• Molecules
  • Favourite alkaloids are C8H10N4O2 and C10H14N2 (Well, I quit on July 2012)
  • I also taste CH3CH2OH in good wines such as Château Peyrines (F-33410 Cadillac, France)
  • I have not tried C17H21NO4 or C2H23NO5 yet
  • Paul Sabatier Reaction: CO2 + 4H2 → CH4 + 2H2O
• Popular science?
  • À vrai dire, je n'aime pas beaucoup le terme « vulgarisation » qui a la même racine que le mot péjoratif « vulgaire ». Il faudrait forger un nouveau terme qui signifierait « rendre accessible avec enthousiasme en excitant la curiosité ».
  • Quanta Magazine
  • Image des mathématiques
  • Stackexchange
• Social mathematics
  • MathOverflow - for researchers
  • Math Stackexchange - for students
• Mathematical collections
  • Digital Library of Mathematical Functions
  • The On-Line Encyclopedia of Integer Sequences
• Blogs
  • What's new - Terrence Tao blog
  • Freakonometrics - Arthur Charpentier blog
  • Research and lecture notes - Fabrice Baudoin blog
• Papers
  • How to write your own Computer Science papers
  • How to write your own Mathematics papers
  • A very bad paper by Claude S. and another bad one by Henri L.
• Computer Science
  • {0,1}^∞ on my blog
  • The Open Problems Project on Computational Geometry and Related Fields
  • LightOn or how to bring light to AI
  • Have you heard about the Gödel prize? and the Turing award?
  • An introduction to Kolmogorov complexity and its applications
  • List of books on combinatorial optimization and information theory (on my blog)
  • Elements of queueing theory: Palm-martingale calculus and stochastic recurrences
  • Daniel J. Bernstein
  • Detexify LaTeX handwritten symbol recognition
• Probability
  • Provocation: «// Si tu ne sais pas ce que c'est que les probabilités, c'est probablement ce qui te manque pour comprendre la physique ! » * « Un homme tirait au sort toutes ses décisions. Il ne lui arriva pas plus de mal qu'aux autres qui réfléchissent. »
    Paul Valéry, Choses Tues, Oeuvres II, Pléiade, p. 505.
    Denis Talay : « Et s'il avait réfléchi en plus de tirer au sort ? » * La méthode probabiliste par Marie Heyvaert et F. Thomas Bruss * The probabilistic method by Noga Alon and Joel H. Spencer * Additive combinatorics by Terence Tao and Van H. Vu * Open problems by Yuval Peres * Open problems by David Aldous * Open problems in Mathematical Physics by Michael Aizenman including probabilistic problems * HomePage of François Baccelli * Perfectly Random Sampling with Markov Chains * Numerical Analysis * Nineteen dubious ways to compute the exponential of a matrix, twenty-five years later by Clive Moler and Charles Van Loan * Volker Strassen, from the law of the iterated logarithm to matrix multiplications * Mathematics & Biology * Uses and Abuses of Mathematics in Biology by Why Is Mathematical Biology So Hard? by Michael C. Reed * Mathematics & Physics * «Le physicien traite les problèmes du véhicule à une roue (la brouette), à deux roues (tilbury ou bicyclette), à trois, à quatre roues. Le mathématicien traite le problème général du véhicule à n roues, n étant entier ou fractionnaire, positif ou négatif, réel ou imaginaire.»
    Henri Bouasse * Free software * For mathematicians (on my Blog) * « Don't forget that Linux became only possible because 20 years of OS research was carefully studied, analyzed, discussed and thrown away. »
    Ingo Molnár * « This is the Unix philosophy: Write programs that do one thing and do it well. Write programs to work together. Write programs to handle text streams, because that is a universal interface. »
    Doug McIlroy * Tanenbaum-Torvalds Debate: Part II, see also the related wikipedia page on this topic * Minds * Beyond pure science: Jean Bricmont and Noam Chomsky * Humanism and Cosmopolitanism: Edward Said and Daniel Barenboim * Englishman: Harold Pinter * Middle East: Avraham Burg and Shlomo Sand * Europe * L'Europe vue par les français d'après Luc Devroye * Literature (or « lis tes ratures// »)
  • Michel Houellebecq (1958 - )
    • «// Alice posait sur nous ce regard à la fois affectueux et légèrement moqueur des femmes qui suivent une conversation entre hommes, cette chose curieuse qui semble toujours hésiter entre la pédérastie et le duel. »
      in //Soumission p. 58 (2015)
    • «// Il avait un cachet “intellectuel de droite” assez séduisant, me dis-je, ça lui assurait une petite singularité à la fac. On peut laisser parler les gens assez longtemps, ils sont toujours intéressés par leur propre discours, mais il faut quand même relancer de temps en temps, un minimum. »
      in //Soumission p. 60 (2015)
  • Alexandre Soljenitsyne (1918 - 2008)
    • «// Peu à peu, j’ai découvert que la ligne de partage entre le bien et le mal ne sépare ni les États ni les classes ni les partis, mais qu’elle traverse le cœur de chaque homme et de toute l’humanité. » * Art * Pablo Picasso (1881 - 1973) * « La inspiración existe, pero tiene que encontrarte trabajando » (”Inspiration exists, but it has to find you working)“
      in //Tomás R. Villasante (1994), Las ciudades hablan: identidades y movimientos sociales en seis metrópolis latinoamericanas. p. 264.
  • Guy Ribes (1948 - )
    • «// Comme pour n'importe quel tableau, chaque faux suppose une recherche. Un peintre, qu'il soit faussaire ou non, est, toute sa vie, un étudiant qui se met à l'école de l'art. Je n'ai pas fait un seul Matisse ou un seul Renoir, je les ai faits en dix exemplaires, jusqu'à ce que je comprenne leur nature et leur sens. On ne peut pas créer une œuvre de cette importance du premier coup. On commet des erreurs, on détruit, on recommence… »
      in //Autoportrait d'un faussaire p. 120 (2015)

• Mathematicians and physicists
  • The probabilistic quartet: Andrey, Joseph, Paul, and Kiyosi
  • Free probability: Eugene P. Wigner and John von Neumann were schoolmates in Budapest and colleagues in Princeton. Their works were connected by Dan-Virgil Voiculescu, a romanian-american mathematician.
  • András Sárközy and Carlo Bruni never wrote a joint paper… (their MR graph distance is 4)
  • Didier Concordet (1962 - )
    • «D'année en année, les étudiants sont de plus en plus jeunes. //» * Roger-Dominique Bakry (1954 - × ) * « Y'a qu'un nombre fini d'idées. » * « À part Cauchy-Schwarz… » and more recently « À part Pythagore… » * « Ce qui compte, en maths, c'est les idées » * « En général, dans un papier, entre l'abstract et le non-sense, il y a l'introduction » * « De toute manière, tous les papiers sont faux, et ça n'est pas grave, car personne ne les lit » * « Tu ferais mieux de te trouver un vrai métier… » * James Clerk Maxwell (1831 - 1879) * «… They say that Understanding ought to work by the rules of right reason. These rules are, or ought to be, contained in Logic; but the actual science of Logic is conversant at present only with things either certain, impossible, or entirely doubtful, none of which (fortunately) we have to reason on. Therefore the true Logic for this world is the Calculus of Probabilities, which takes account of the magnitude of the probability (which is, or which ought to be in a reasonable man's mind). This branch of Math., which is generally thought to favour gambling, dicing, and wagering, and therefore highly immoral, is the only “Mathematics for Practical Men,” as we ought to be. …// James Clerk Maxwell (1850) Letter to Lewis Campbell; reproduced in L. Campbell and W. Garrett, The Life of James Clerk Maxwell, Macmillan, 1881, page 80.
  • Mark Kac (1914 - 1984)
    • «I prefer concrete things and I don't like to learn more about abstract stuff than I absolutely have to. //» * Henri Poincaré (1854 - 1912) * À propos de la loi normale du théorème central limite, désigné sous le nom de loi des erreurs à l'époque : « Cette loi ne s'obtient pas par des déductions rigoureuses ; plus d’une démonstration qu’on a voulu en donner est grossière, entre autres celle qui s’appuie sur l’affirmation que la probabilité des écarts est proportionnelle aux écarts. Tout le monde y croit cependant, me disait un jour M. Lippmann, car les expérimentateurs s’imaginent que c’est un théorème de mathématiques, et les mathématiciens que c’est un fait expérimental. » In //Le calcul des Probabilités (1896) p. 149). Comme le dit le physicien Oriol Bohigas, de nos jours, nous savons que c'est à la fois un fait expérimental et un théorème de mathématiques !
  • Bruno de Finetti (1906 - 1985)
    • «…Mathematics is not by now a field already explored, just to learn and pass on to posterity as it is. It is always progressing, it is enriching and lightening itself, it is a lively and vital creature, in full development and just for these reasons I love it, I study it and I wish to devote my life to it…»
  • Philippe Biane (1962 - )
    • Les probabilités et le mouvement brownien (Vidéo, magnifique cravate)
  • Vladimir Arnold (1937 - 2010)
    • La mathématique expérimentale (Vidéo)
    • « Les mathématiques ne sont qu'un chapitre de la physique ! »
  • David Louis Goodstein (1939 - 2024)
    • «// Ludwig Boltzmann, who spent much of his life studying statistical mechanics, died in 1906, by his own hand. Paul Ehrenfest, carrying on the work, died similarly in 1933. Now it is our turn to study statistical mechanics. Perhaps it will be wise to approach the subject cautiously.// » (Opening lines of “States of Matter”)
  • Jean-Pierre Serre (1926 - )
    • How to write mathematics badly (Video)
  • Bernard Beauzamy (1947 - )
    • Les erreurs en mathématiques (Vidéo)
    • Méthodes mathématiques pour l'évaluation de la fiabilité des équipements (Vidéo)
    • Les mathématiques du réel
  • James Harris Simons (1938 - )
    • James Simons (full length interview) - Numberphile (Video)
  • Jean-Philippe Bouchaud (1962 - )
    • De la physique statistique à la gestion d'actifs financiers (Vidéo)
    • De la physique statistique aux sciences sociales : les défis de la pluridisciplinarité (Vidéo)
  • Marc Potters
    • Innovation: Stories of Start-ups issued from Fundamental Research : CFM aujourd'hui (2017) (Vidéo)
  • Bernard Derrida (1952 - )
    • Physique statistique (Vidéo)
  • Enrico Fermi (1901 - 1954)
    • «// There are several categories of scientists in the world; those of second or third rank do their best but never get very far. Then there is the first rank, those who make important discoveries, fundamental to scientific progress. But then there are the geniuses, like Galilei and Newton. Majorana was one of these. » 1938, about Ettore Majorana * Ludwig Boltzmann (1844 - 1906) * « … If you ask me about my innermost conviction whether our century will be called the century of iron or the century of steam or electricity, I answer without hesitation: It will be called the century of the mechanical view of Nature, the century of Darwin. … » * John Forbes Nash Jr. (1928 - 2015) * « The ideas I had about supernatural beings came to me the same way that my mathematical ideas did. So I took them seriously. » * Gian-Carlo Rota (1932 - 1999) * Ten Lessons I Wish I Had Been Taught Notices on the AMS 44 (1997) * « Don't fight with success » * « You should only listen to advice that you do not have to follow » * Paul Halmos (1916 - 2006) * « Don't just read it; fight it! Ask your own questions, look for your own examples, discover your own proofs. Is the hypothesis necessary? Is the converse true? What happens in the classical special case? What about the degenerate cases? Where does the proof use the hypothesis? » * Godfrey Harold Hardy (1877 - 1947) * « The mathematician’s patterns, like the painter’s or the poet’s must be beautiful; the ideas like the colours or the words, must fit together in a harmonious way. Beauty is the first test: there is no permanent place in the world for ugly mathematics. » * John von Neumann (1903 - 1957) * «If people do not believe that mathematics is simple, it is only because they do not realize how complicated life is. » * The Mathematician (1947) * Barry Simon (1946 - ), quoting Freeman Dyson (1923 - ), quoting Godfrey Harold Hardy (1877 - 1947) * « Young men should prove theorems, old men should write books. » * Hermann Weyl (1885 - 1955) * « My work always tried to unite the truth with the

beautiful, but when I had to choose one or the other, I usually chose the beautiful. » * Edward Brian Davies (1944 - 2025) * « Studying non-self-adjoint operators is like being a vet rather than a doctor: one has to acquire a much wider range of knowledge, and to accept that one cannot expect to have as high a rate of success when confronted with particular cases. It comprises a collection of methods, each of which is useful for some class of such operators. » * Daniel W. Stroock (1940 - 2025) * « Mathematics is one, and possibly the only, human endeavor for which there is a widely, if not universally, recognized criterion with which to determine truth. For this reason, mathematicians can avoid some of the interminable disputes which plague other fields. On the other hand, I sometimes wonder whether the most interesting questions are not those for which such disputes are inevitable. » * Terence Chi-Shen Tao (陶哲軒) (1975 - ) * Soft analysis, hard analysis, and the finite convergence principle * Research blog · Advice on writing papers · Career advice · On time management * Sir William Timothy Gowers (1963 - ) * The polymath project on his blog * The tricki project * The two cultures of mathematics * William P. Thurston (1946 - 2012) * On proof and progress in mathematics * Others * Napoléon Bonaparte (1769 - 1821) * « Géomètre de première catégorie, Laplace n'a pas tardé à se montrer un administrateur plus que médiocre ; de son premier travail nous avons immédiatement compris que nous nous étions trompés. Laplace ne traitait aucune question d'un bon point de vue : il cherchait des subtilités de partout, il avait seulement des idées problématiques et enfin il portait l'esprit de l'infiniment petit jusque dans l'administration. » Bulletin de Napoléon à la démission de Pierre-Simon de Laplace (1749 - 1827) du poste de Ministre de l'intérieur, après six semaines. * Georges Brassens (1921 - 1981) * « Mais sans technique, un don n'est rien ♫ Qu'une sale manie… » in //Le mauvais sujet repenti

• Antonio Gramsci (1891 - 1937) (also attributed to Romain Rolland)
  • « I’m a pessimist because of intelligence, but an optimist because of will. » in Letter from Prison (19 December 1929);
• Audrey Dussutour (1977 - )
  • « La recherche est comme une plante, dont la fleur serait la recherche appliquée, et la racine la recherche fondamentale. »
• Some curiosities
• How to select the number of classes in a histogram? Californian way and Parisian way
• Wikipedia's Category on Mathematics paradoxes
• Ig Nobel Prize
• Money
• Who said that mathematicians do not like money? It seems at least that the converse is false…