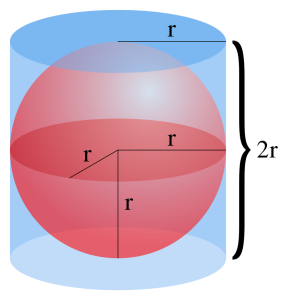
Archimedes theorem. Archimedes (Ἀρχιμήδης) of Syracuse (-287 – -212) is one of the greatest minds of all times. One of his discoveries is as follows : if we place a sphere in the tightest cylinder, then the surface of the sphere and of the cylinder are the same, and more generally, if we cut the whole in two pieces by any perpendicular horizontal plane, then this remains for each pieces : the surface of the spherical cap is equal to the surface of the corresponding slice of cylinder. Archimedes was so proud of it that he put the picture of it on his tombstone. This allowed his admirer Marcus Tullius Cicero (-106 – -43) to identify the tomb, in -75, almost 150 years after the murder of Archimedes by a Roman soldier during the siege of Syracuse.
The Archimedes theorem allows to recover the formula for the surface of the sphere : if the sphere has radius $r$, then the surface of the cylinder is $2\pi r\times 2r=4\pi r^2$. The cutting plane part of the Archimedes theorem says that the uniform distribution on the sphere, when projected on the vertical diameter, gives the uniform distribution on the diameter. Archimedes used antic geometrical methods. Nowadays, with the development of modern analytic and probabilistic tools, we can prove easily an extension of his theorem to arbitrary dimension. More precisely, let $(X_1,\ldots,X_n)$ be a random vector of $\mathbb{R}^n$, $n\geq3$, uniformly distributed on the sphere $\mathbb{S}^{n-1}$. Then its projection $(X_1,\ldots,X_{n-2})$ on $\mathbb{R}^{n-2}$ is uniform on the unit ball of $\mathbb{R}^{n-2}$. Indeed, since $$(X_1,\ldots,X_n)\overset{\mathrm{d}}{=}\frac{Z}{\|Z\|}=\frac{(Z_1,\ldots,Z_n)}{\sqrt{Z_1^2+\cdots+Z_n^2}}$$where $Z=(Z_1,\ldots,Z_n)\sim\mathcal{N}(0,I_n)$, we get, for all $1\leq k\leq n$,
$$\begin{align*}\|(X_1,\ldots,X_k)\|^2
&=X_1^2+\cdots+X_k^2\\
&\overset{\mathrm{d}}{=}
\frac{Z_1^2+\cdots+Z_k^2}{Z_1^2+\cdots+Z_k^2+Z_{k+1}^2+\cdots+Z_n^2}\\
&=\frac{A}{A+B}\\
&\sim\mathrm{Beta}\Bigr(\frac{k}{2},\frac{n-k}{2}\Bigr),\end{align*}$$ where the last step comes from the fact that $\frac{A}{A+B}\sim\mathrm{Beta}(\frac{a}{2},\frac{b}{2})$ when $$A\sim\chi^2(a)=\Gamma\Bigr(\frac{a}{2},\frac{1}{2}\Bigr)\quad\text{and}\quad B\sim\chi^2(b)=\Gamma\Bigr(\frac{b}{2},\frac{1}{2}\Bigr)\quad\text{are independent}.$$Recall that the law $\mathrm{Beta}(\alpha,\beta)$ has density proportional to $t\in[0,1]\mapsto t^{\alpha-1}(1-t)^{\beta-1}$, which is a power when $\beta=1$. In particular, in the special case where $k=n-2$, we find $$\mathrm{Beta}\Bigr(\frac{k}{2},\frac{n-k}{2}\Bigr)=\mathrm{Beta}\Bigr(\frac{n}{2}-1,1\Bigr),$$and this law has a power density, proportional to $t\in[0,1]\mapsto t^{n/2-2}$. Now, a rotationally invariant random vector $X’$ of $\mathbb{R}^{n-2}$ is uniformly distributed on the unit ball of $\mathbb{R}^{n-2}$ iff $\|X’\|$ has density proportional to $r\in[0,1]\mapsto r^{n-3}$, in other words $\|X’\|^2$ has density proportional to $t\in[0,1]\mapsto\sqrt{t}^{n-3}/\sqrt{t}=t^{n/2-2}$, which matches the Beta law above.
Reverse Archimedes theorem. It states that if $Z_1,\ldots,Z_n$ are i.i.d. $\mathcal{N}(0,1)$, $n\geq1$, and if $E$ is exponential of unit mean independent of $Z_1,\ldots,Z_n$, then the random vector $$
\frac{(Z_1,\ldots,Z_n)}{\sqrt{Z_1^2+\cdots+Z_n^2+2E}}
$$ is uniformly distributed on the unit ball of $\mathbb{R}^n$. To see it, it suffices to use an extended Gaussian sequence $(Z_1,\ldots,Z_{n+2})\sim\mathcal{N}(0,I_{n+2})$, the Archimedes principle, and the observation that $$Z_{n+1}^2+Z_{n+2}^2\sim\chi^2(2)=\Gamma\Bigr(\frac{2}{2},\frac{1}{2}\Bigr)=\mathrm{Exp}\Bigr(\frac{1}{2}\Bigr)\sim 2E.$$ The reverse Archimedes principle reveals that the uniform law on the ball concentrates, in high dimension, around the extremal sphere at its edge. Indeed, by the law of large numbers,$$\frac{\sqrt{Z_1^2+\cdots+Z_n^2}}{\sqrt{Z_1^2+\cdots+Z_n^2+2E}}=\frac{1}{\sqrt{1+O\bigr(\frac{1}{n}\bigr)}}\underset{n\to\infty}{\longrightarrow}1\quad\text{almost surely}.$$This is an instance of the thin-shell phenomenon for convex bodies. From this point of view, in high dimension $n$, the sphere of radius $\sqrt{n}$ behaves approximately as an isotropic convex body.
Note. The Archimedes theorem on the sphere and the cylinder is sometimes referred to as the Archimedes principle. But this last term is more classically used for the fact that a body at rest in a fluid is acted upon by a force pushing upward called the buoyant force, equal to the weight of the fluid that the body displaces, related to the famous Eurêka! These are distinct discoveries.

Further reading.
- Archimedes of Syracuse
On the Sphere and Cylinder
Two volumes (-225) - Bernard Beauzamy
Archimedes’ Modern Works
Real Life Mathematics, Société de Calcul Mathématique (2012) - Gérard Letac
From Archimedes to statistics: the area of the sphere - Jim Pitman and Nathan Ross
Archimedes, Gauss, and Stein
Notices American Mathematical Society 59(10) 1416-1421 (2012) - Author of this blog
Phénomènes de grande dimension
Notes de cours – École normale supérieure (2024) - Author of this blog
The Funk-Hecke formula
Libres pensées d’un mathématicien ordinaire (2021) - Author of this blog
Central limit theorem for convex bodies
Libres pensées d’un mathématicien ordinaire (2011)

Modern times. The reasoning above involving a Beta law is actually a very special aspect of a more general and deeper probabilistic structure involving the Dirichlet law, a generalizatoin of the Euler Beta law, defined using the Euler Gamma law. More precisely, for real parameters $a_1>0,\ldots,a_n>0$, the law $\mathrm{Dirichlet}(a_1,\ldots,a_n)$ is the law of the random vector
$$(D_1,\ldots,D_n):=\frac{(G_1,\ldots,G_n)}{G_1+\cdots+G_n}$$of $\mathbb{R}^n$, where $G_1,\ldots,G_n$ are independent with $G_i\sim\mathrm{Gamma}(a_i,\lambda)$, for an arbitrary scaling parameter $\lambda>0$. We can safely take without loss of generality $\lambda=1$. The support of this law is the simplex of discrete probability distributions with $n$ atoms $$\Delta_n:=\{(p_1,\ldots,p_n):p_1\geq0,\ldots,p_n\geq0,p_1+\cdots+p_n=1\}\subset[0,1]^n.$$ Its density is
$$
(x_1,\ldots,x_{n-1})\mapsto
\frac{\Gamma(a_1+\cdots+a_n)}{\Gamma(a_1)\cdots\Gamma(a_n)}
\prod_{i=1}^{n-1}x_i^{a_i-1}\Bigr(1-\sum_{i=1}^{n-1}x_i\Bigr)^{a_n-1}
\mathbf{1}_{(x_1,\ldots,x_{n})\in\Delta_n}.
$$ Moreover, for all $1\leq i\leq n$, the $i^{\mathrm{th}}$ component follows a Beta law :
$$\frac{G_i}{G_1+\cdots+G_n}\sim\mathrm{Beta}(a_i,a_1+\cdots+a_n-a_i).$$ The Dirichlet law structure is stable by summation by blocks. More precisely, for any partitition $I_1,\ldots,I_k$ of the finite set $\{1,\ldots,n\}$ into non-empty subsets or blocks, we have
$$
\Bigr(\sum_{i\in I_1}D_i,\ldots,\sum_{i\in I_k}D_i\Bigr)
\sim\mathrm{Dirichlet}\Bigr(\sum_{i\in I_1}a_i,\ldots,\sum_{i\in I_k}a_i\Bigr),$$ and for any non-empty subset $I$ of $\{1,\ldots,n\}$, $$\sum_{i\in I}D_i\sim\mathrm{Beta}\Bigr(\sum_{i\in I}a_i,\sum_{i\not\in I}a_i\Bigr).$$The Dirichlet law plays an important role for spatial points processes, stochastic simulation, as well as in Statistics due to their Bayesian duality with multinomial laws. If $U_1,\ldots,U_n$ are independent uniform random variables on $[0,1]$, and if $U_{(0)}\leq\cdots\leq U_{(n)}$ is their non-decreasing reordering, known as the order statistics, then, denoting $U_{(0)}:=0$ and $U_{(n+1)}:=1$, $$(U_{(1)}-U_{(0)},\ldots,U_{(n+1)}-U_{(n)})\overset{\mathrm{d}}{=}\frac{(E_1,\ldots,E_{n+1})}{E_1+\cdots+E_{n+1}}\sim\mathrm{Dirichlet}(1,\ldots,1),$$ where $E_1,\ldots,E_{n+1}$ are independent and identically distributed exponential random variables (with arbitrary parameter). This fact is at the heart of Poisson point processes.
Another important side of what we used is the link between chi-square laws and Gamma laws. In terms of probabilistic culture and structure, there are two basic facts. The first one is $$\chi^2(1):=\Bigr(\mathcal{N}(0,1)\Bigr)^2=\mathrm{Gamma}\Bigr(\frac{1}{2},\frac{1}{2}\Bigr)$$ while the second one is the additivity related to the Gamma shape parameter $$\mathrm{Gamma}(a,\lambda)*\mathrm{Gamma}(b,\lambda)=\mathrm{Gamma}(a+b,\lambda).$$ This gives the important fact $$\chi^2(n)=(\chi^2(1))^{*n}=\Gamma\Bigr(\frac{n}{2},\frac{1}{2}\Bigr).$$ In particular the heart of the Box-Muller simulation algorithm involves the special case $$\chi^2(2)=\mathrm{Gamma}\Bigr(1,\frac{1}{2}\Bigr)=\mathrm{Expo}\Bigr(\frac{1}{2}\Bigr)=-2\log(\mathrm{Uniform}[0,1]).$$
Leave a Comment